题目内容
已知f（x2+2）=x4+4x2，求f（x）的解析式．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：令x2+2=t，则：x2=t-2，（t≥2），从而f（t）=（t-2）2+4（t-2），整理替换即可．
解答：
解：令x2+2=t，则：x2=t-2，（t≥2），
∴f（t）=（t-2）2+4（t-2）
=t2-4，
∴f（x）=x2-4（x≥2）．
∴f（t）=（t-2）2+4（t-2）
=t2-4，
∴f（x）=x2-4（x≥2）．
点评：本题考查了求函数的解析式问题，换元法是常用的方法之一，本题属于基础题．
练习册系列答案
相关题目
已知函数f（x）=sinx，下面结论错误的是（ ）
| A、f（x）的最小正周期是2π | ||||||||
B、f（x）在[0，
| ||||||||
C、f（x）[
| ||||||||
| D、f（x）的值域为[-1，1] |
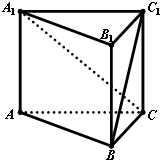在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形．
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜