题目内容
已知抛物线C：y2=4x，直线l过点T（t，0）且与抛物线相交于A、B两点，O为坐标原点，若∠AOB为锐角，则t的取值范围是（ ）
| A、0＜t＜4 |
| B、0＜t＜2 |
| C、t≥2 |
| D、t＞4或t＜0 |
考点：抛物线的简单性质
专题：综合题,圆锥曲线的定义、性质与方程
分析：由题意设出过T点的直线方程为x=my+t，联立直线方程和抛物线方程，利用根与系数关系得到A，B两点的横纵坐标的积，由
•
＞0求得t的范围．
| OA |
| OB |
解答：
解：由题意设直线l的方程为x=my+t，
与y2=4x联立，得y2-4my-4t=0，
设A（x1，y1），B（x2，y2），
则y1+y2=4m，y1y2=-4t，x1x2=-4tm2+4tm2+t2=t2．
由
•
=x1x2+y1y2=t2-4t＞0，
解得：t＞4或t＜0．
故选：D．
与y2=4x联立，得y2-4my-4t=0，
设A（x1，y1），B（x2，y2），
则y1+y2=4m，y1y2=-4t，x1x2=-4tm2+4tm2+t2=t2．
由
| OA |
| OB |
解得：t＞4或t＜0．
故选：D．
点评：本题考查了直线与圆锥曲线的关系，涉及直线与圆锥曲线关系问题，常采用联立直线与圆锥曲线，化为关于x的一元二次方程，利用根与系数关系求解，是中档题．
练习册系列答案
相关题目
数列{an}满足a1=1，且对于任意的n∈N*都有an+1=an+a1+n，则
+
+…+
等于（ ）
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2014 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示，程序框图输出的所有实数对（x，y）所对应的点都在函数（ ）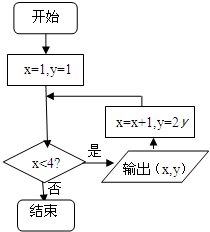
| A、y=x+1的图象上 |
| B、y=2x的图象上 |
| C、y=2x的图象上 |
| D、y=2x-1的图象上 |
数列{an}，满足对任意的n∈N+，均有an+an+1+an+2为定值．若a7=2，a9=3，a98=4，则数列{an}的前100项的和S100=（ ）
| A、132 | B、299 |
| C、68 | D、99 |