题目内容
在直角坐标系xOy中,以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ2-4
ρcos(θ-
)+6=0.
(Ⅰ)求C的参数方程;
(Ⅱ)若点P(x,y)在曲线C上,求x+y的最大值和最小值.
| 2 |
| π |
| 4 |
(Ⅰ)求C的参数方程;
(Ⅱ)若点P(x,y)在曲线C上,求x+y的最大值和最小值.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(Ⅰ)直接根据极坐标和直角坐标方程互化公式求解得到其直角坐标方程,然后,再将其化为参数方程即可,
(Ⅱ)依据曲线C的参数方程,可以设该点P的三角形式,然后,借助于三角函数的最值求解.
(Ⅱ)依据曲线C的参数方程,可以设该点P的三角形式,然后,借助于三角函数的最值求解.
解答:
解:(I)C的极坐标方程化为ρ2-4ρcosθ-4ρsinθ+6=0,
∴C的直角坐标方程是x2+y2-4x-4y+6=0,
即(x-2)2+(y-2)2=2,C的参数方程是
,φ是参数;…(5分)
(II)∵点P(x,y)在曲线C上,
由
(φ是参数)得到
x+y=4+2sin(φ+
),
∴x+y的最大值是6,最小值是2.…(10分)
∴C的直角坐标方程是x2+y2-4x-4y+6=0,
即(x-2)2+(y-2)2=2,C的参数方程是
|
(II)∵点P(x,y)在曲线C上,
由
|
x+y=4+2sin(φ+
| π |
| 4 |
∴x+y的最大值是6,最小值是2.…(10分)
点评:本题重点考查极坐标方程和直角坐标方程、参数方程的互化、三角函数的最值等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知两个单位向量
,
的夹角为60°,
=(1-t)
+t
,若
•
=-
,则实数t的取值是( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
设二项式(x-
)4的展开式中常数项为A,则A=( )
| 1 | |||
|
| A、-6 | B、-4 | C、4 | D、6 |
数列{an}满足an+1=
,若a1=
,则a2015=( )
|
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=x|x-a|,若对?x1,x2∈[3,+∞),x1≠x2,不等式
>0恒成立,则实数a的取值范围是( )
| f(x1)-f(x2) |
| x1-x2 |
| A、(-∞,-3] |
| B、[-3,0) |
| C、(-∞,3] |
| D、(0,3] |

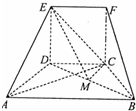 在如图所示的几何体中,四边形CDEF为正方形,ABCD为等腰梯形,AB∥CD,BD=2
在如图所示的几何体中,四边形CDEF为正方形,ABCD为等腰梯形,AB∥CD,BD=2