题目内容
已知F1,F2是双曲线
-
=1(a>0,b>0)的两个焦点,点P是该双曲线和圆x2+y2=a2+b2的一个交点,若sin∠PF1F2=2sin∠PF2F1,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:
分析:由已知条件推导出△PF1F2中,|OP|=c=
|F1F2|,∠F1PF2=90°,|PF1|=2a,|PF2|=4a,由此能求出双曲线的离心率.
| 1 |
| 2 |
解答:
解:∵F1,F2是双曲线
-
=1(a>0,b>0)的两个焦点,
∴双曲线的焦点坐标为F1(-c,0)、F2(c,0),其中c=
,
∵圆方程为x2+y2=a2+b2,即x2+y2=c2,
∴该半径等于c,且圆经过F1和F2,
∵点P是双曲线
-
=1与圆x2+y2=a2+b2的交点,
∴△PF1F2中,|OP|=c=
|F1F2|,∴∠F1PF2=90°,
∵sin∠PF1F2=2sin∠PF2F1,
∴
=
,∴|PF2|=2|PF1|.
设|PF1|=x,则|PF2|=2x,
由双曲线性质得2x-x=x=2a,
∴|PF1|=2a,则|PF2|=4a,
由勾股定理得(2a)2+(4a)2=(2c)2,
解得c=
a,
∴e=
=
.
故选:B.
| x2 |
| a2 |
| y2 |
| b2 |
∴双曲线的焦点坐标为F1(-c,0)、F2(c,0),其中c=
| a2+b2 |
∵圆方程为x2+y2=a2+b2,即x2+y2=c2,
∴该半径等于c,且圆经过F1和F2,
∵点P是双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴△PF1F2中,|OP|=c=
| 1 |
| 2 |
∵sin∠PF1F2=2sin∠PF2F1,
∴
| |PF2| |
| 2c |
| 2|PF1| |
| 2c |
设|PF1|=x,则|PF2|=2x,
由双曲线性质得2x-x=x=2a,
∴|PF1|=2a,则|PF2|=4a,
由勾股定理得(2a)2+(4a)2=(2c)2,
解得c=
| 5 |
∴e=
| c |
| a |
| 5 |
故选:B.
点评:本题考查双曲线的离心率的求法,是中档题,解题时要认真审题,注意双曲线简单性质的灵活运用.

练习册系列答案
相关题目
已知两条直线m,n和平面α,且m在α内,n在α外,则“n∥α”是“m∥n”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知i是虚数单位,则
=( )
| 2-i |
| 1+2i |
| A、-i | ||||
B、
| ||||
| C、-1 | ||||
D、
|
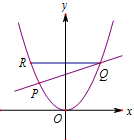 如图,设直线l:y=kx+
如图,设直线l:y=kx+