题目内容
阅读下列一段材料,然后解答问题:对于任意实数x,符号[x]表示“不超过x的最大整数”,在数轴上,当x是整数,[x]就是x,当x不是整数时,[x]是点x左侧的第一个整数点,这个函数叫做“取整函数”,也叫高斯(Gauss)函数.如[-2]=-2,[-1.5]=-2,[2.5]=2.求[log2
]+[log2
]+[log2
]+[log21]+[log22]+[log23]+[log24]的值为( )
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、-1 | B、-2 | C、0 | D、1 |
考点:对数的运算性质
专题:函数的性质及应用
分析:根据“取整函数”的定义即可求得答案.
解答:
解:log2
=-2,-2<log2
<-1,log2
=-1,log21=0,log22=1,1<log23<2,log24=2,
由“取整函数”的定义可得,
[log2
]+[log2
]+[log2
]+[log21]+[log22]+[log23]+[log24]
=-2-2-1+0+1+1+2=-1.
故选:A.
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
由“取整函数”的定义可得,
[log2
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
=-2-2-1+0+1+1+2=-1.
故选:A.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意对数函数的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
现有90kg货物需要装成5箱,要求每一箱所装货物的重量不超过其它任一箱所装货物重量的2倍.若某箱所装货物的重量为x kg,则x的取值范围是( )
| A、10≤x≤18 |
| B、10≤x≤30 |
| C、18≤x≤30 |
| D、15≤x≤30 |
三个数30.4,0.43,30.3的大小关系( )
| A、0.43<30.3<30.4 |
| B、0.43<30.4<30.3 |
| C、30.3<30.4<0.43 |
| D、30.3<0.43<30.4 |
函数f(x)=
的值域是( )
| 3x-1 |
| 3x+1 |
| A、(-1,1) |
| B、[-1,1] |
| C、(-1,1] |
| D、[-1,1) |
已知函数f(x)=
,若f(x0)=3,则x0的值为( )
|
| A、x0=0 |
| B、x0=8 |
| C、x0=8或x0=0 |
| D、x0=6或x0=0 |
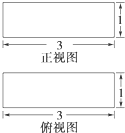
在具有如图所示的正视图和俯视图的几何体中,体积最小的几何体的表面积为 ( )

| A、13 | ||
B、7+3
| ||
C、
| ||
| D、14 |
