题目内容
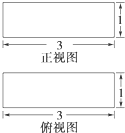
在具有如图所示的正视图和俯视图的几何体中，体积最小的几何体的表面积为 （ ）
| A、13 | ||
B、7+3
| ||
C、
| ||
| D、14 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据几何体的三视图，得该几何体可能是什么图形，从而进行解答．
解答：
解：由正视图和俯视图知，
该几何体可能是四棱柱，或是水平放置的三棱柱，或是水平放置的圆柱；
其中三棱柱的体积最小，此时三棱柱的高为3，底面为腰长是1的等腰直角三角形，如图所示；
∴它的表面积为S=1×3+1×3+
×1×1+
×1×1+
×3=7+3
．
故选：B．
该几何体可能是四棱柱，或是水平放置的三棱柱，或是水平放置的圆柱；
其中三棱柱的体积最小，此时三棱柱的高为3，底面为腰长是1的等腰直角三角形，如图所示；
∴它的表面积为S=1×3+1×3+
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故选：B．
点评：本题考查了空间几何体的三视图的应用问题，也考查了求几何体表面积的问题，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
命题“?x∈R，2x+x2≤1”的否定是（ ）
| A、?x∈R，2x+x2＞1，假命题 |
| B、?x∈R，2x+x2＞1，真命题 |
| C、?x∈R，2x+x2＞1，假命题 |
| D、?x∈R，2x+x2＞1，真命题 |
如图，直四棱柱ABCD-A1B1C1D1的底面是梯形，AB∥CD，AD⊥DC，CD=2，DD1=AB=1，P、是CC1的中点，求证：PB∥面AD1C．（用两种方法）