题目内容
2.(1)已知椭圆的离心率为$\frac{{\sqrt{2}}}{2}$,准线方程为x=±8,求该椭圆的标准方程(2)求与双曲线x2-2y2=2有公共渐近线,且过点M(2,-2)的双曲线方程.
分析 (1)由题意,$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{{a}^{2}}{c}=8}\end{array}\right.$,即可求该椭圆的标准方程;
(2)设出双曲线方程,代入点的坐标求解即可.
解答 解:(1)由题意,$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{{a}^{2}}{c}=8}\end{array}\right.$,∴a=$4\sqrt{2}$,c=4,b=4,
∴椭圆的标准方程为$\frac{x^2}{32}+\frac{y^2}{16}=1$;
(2)所求双曲线与双曲线x2-2y2=2有公共渐近线,
所以设双曲线为:x2-2y2=m,过点M(2,-2)
则4-8=m,m=-4.
所求双曲线方程为:x2-2y2=-4.即$\frac{y^2}{2}-\frac{x^2}{4}=1$.
点评 本题考查椭圆、双曲线方程的求法,设双曲线方程是简化解题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
13.在△ABC中,若b2+c2-a2=bc,则角A的值为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
14.复数$z=\frac{10i}{3+i}$(i为虚数单位)的虚部为( )
| A. | 1 | B. | 3 | C. | -3 | D. | $\frac{15}{4}$ |
12.某程序框图如图所示,若运行该程序后输出的值是$\frac{9}{19}$,则整数t的值是( )


| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
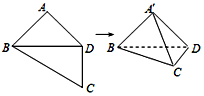 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).