题目内容
12.已知函数$f(x)=\sqrt{3}sinxcosx-{sin^2}x$,则f(x)的最小正周期为π;单调减区间为[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.分析 利用两角和差的正弦公式化简函数的解析式,再利用正弦函数的最小正周期以及单调性得出结论.
解答 解:∵函数$f(x)=\sqrt{3}sinxcosx-{sin^2}x$=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1-cos2x}{2}$=sin(2x+$\frac{π}{6}$)-$\frac{1}{2}$,
∴函数的最小正周期为$\frac{2π}{2}$=π,令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,
故函数的减区间为[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.
故答案为:π;[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.
点评 本题主要考查两角和差的正弦公式的应用,求正弦函数的最小正周期以及单调性,属于基础题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
7. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|ω|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|ω|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|ω|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|ω|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )| A. | 函数f(x)的最小正周期为2π | |
| B. | 函数f(x)的图象关于点(-$\frac{5π}{12}$.0)对称 | |
| C. | 将函数f(x)的图象向左平移$\frac{x}{6}$个单位得到的函数图象关于y轴对称 | |
| D. | 函数f(x)的单调递增区间是[kx+$\frac{7π}{12}$,kπ+$\frac{13π}{12}$],(k∈Z) |
4.在棱长为1正方体ABCD-A1B1C1D1中,点E,F,G分别为DD1,BD,BB1的中点,则EF,CG所成角的余弦值为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{15}$ | C. | $\frac{{\sqrt{15}}}{5}$ | D. | $\frac{{\sqrt{15}}}{15}$ |
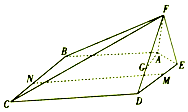 如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.
如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.