题目内容
正项数列{an}满足a1=1,a2=2,又数列{
}是以
为公比的等比数列,则使得不等式
+
+…+
<1280成立的最大整数n为 .
| anan+1 |
| ||
| 2 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2n+1 |
考点:等比数列的性质
专题:综合题,等差数列与等比数列
分析:确定数列{a2n-1}是以a1=1为首项,2-1为公比的等比数列,数列{a2n}是以a2=2为首项,2-1为公比的等比数列,再利用等比数列的求和公式,即可求得结论.
解答:
解:∵a1=1,a2=2,∴
=
.
又{
}是以
为公比的等比数列,
∴
=21-
.
∴anan+1=22-n,∴
=2-1=
.
∴数列{a2n-1}是以a1=1为首项,2-1为公比的等比数列,∴a2n-1=21-n.∴
=2n-1.
数列{a2n}是以a2=2为首项,2-1为公比的等比数列,∴a2n=22-n.∴
=2n-2.
∴
+
+…+
=(20+2+22+…+2n)+(2-1+20+21+…+2n-2)
=2n+1-1+
(2n-1)=5•2n-1-
不等式
+
+…+
<1280,化为5•2n-1-
<1280,
∵29=502,28=256.
∴n-1<9,解得n<10.
因此使得不等式
+
+…+
<1280成立的最大整数n为9.
故答案为:9.
| a1a2 |
| 2 |
又{
| anan+1 |
| ||
| 2 |
∴
| anan+1 |
| n |
| 2 |
∴anan+1=22-n,∴
| an+1an+2 |
| anan+1 |
| an+2 |
| an |
∴数列{a2n-1}是以a1=1为首项,2-1为公比的等比数列,∴a2n-1=21-n.∴
| 1 |
| a2n-1 |
数列{a2n}是以a2=2为首项,2-1为公比的等比数列,∴a2n=22-n.∴
| 1 |
| a2n |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2n+1 |
=2n+1-1+
| 1 |
| 2 |
| 3 |
| 2 |
不等式
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2n+1 |
| 3 |
| 2 |
∵29=502,28=256.
∴n-1<9,解得n<10.
因此使得不等式
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2n+1 |
故答案为:9.
点评:本题考查了等比数列的通项公式及其前n项和公式、分奇数和偶数项分别为等比数列的数列的通项公式及其前n项和公式等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
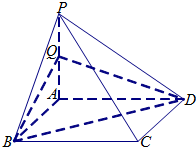 如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.