题目内容
学校举行定点投篮比赛,规定每人投篮4次,投中一球得2分,没有投中得0分,假设每次投篮投中与否是相互独立的.已知小明每次投篮投中的概率都是
.
(1)求小明在投篮过程中直到第三次才投中的概率;
(2)求小明在4次投篮后的总得分ξ的分布列和期望.
| 1 |
| 3 |
(1)求小明在投篮过程中直到第三次才投中的概率;
(2)求小明在4次投篮后的总得分ξ的分布列和期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(1)设小明在第i次投篮投中为事件Ai,则第三次投篮时首次投中的概率为:p=P(
)•P(
)•P(A3),由此能求出结果.
(2)由题意知ξ=0、2、4、6、8,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
. |
| A1 |
. |
| A2 |
(2)由题意知ξ=0、2、4、6、8,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答:
解:设小明在第i次投篮投中为事件Ai,则P(Ai)=
,P(
)=1-
=
,
则第三次投篮时首次投中的概率为:
p=P(
)•P(
)•P(A3)=
•
•
=
.
(2)由题意知ξ=0、2、4、6、8,
P(ξ=0)=(
)4=
,
P(ξ=2)=
(
)(
)3=
,
P(ξ=4)=
(
)2(
)2=
,
P(ξ=6)=
(
)3(
)=
,
P(ξ=8)=(
)4=
,
∴ξ的分布列为:
∴Eξ=0×
+2×
+4×
+6×
+8×
=
.
| 1 |
| 3 |
| Ai |
| 1 |
| 3 |
| 2 |
| 3 |
则第三次投篮时首次投中的概率为:
p=P(
. |
| A1 |
. |
| A2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
(2)由题意知ξ=0、2、4、6、8,
P(ξ=0)=(
| 2 |
| 3 |
| 16 |
| 81 |
P(ξ=2)=
| C | 1 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 32 |
| 81 |
P(ξ=4)=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
P(ξ=6)=
| C | 3 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 81 |
P(ξ=8)=(
| 1 |
| 3 |
| 1 |
| 81 |
∴ξ的分布列为:
| ξ | 0 | 2 | 4 | 6 | 8 | ||||||||||
| P |
|
|
|
|
|
| 16 |
| 81 |
| 32 |
| 81 |
| 8 |
| 27 |
| 8 |
| 81 |
| 1 |
| 81 |
| 8 |
| 3 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
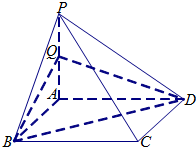 如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,Q是PA的中点. 如图所示,在△ABC中,AB=AC=3,BC=2,B的平分线交过点A且与BC平行的线交于点D,求△ABD的面积.
如图所示,在△ABC中,AB=AC=3,BC=2,B的平分线交过点A且与BC平行的线交于点D,求△ABD的面积.