题目内容
| 1 |
| n(n+1) |
考点：数列的求和
专题：等差数列与等比数列
分析：利用裂项求和法求解．
解答：
解：∵
=
-
，
∴
的前n项和：
S=1-
+
-
+…+
-
=1-
=
．
故答案为：
．
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| n(n+1) |
S=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
故答案为：
| n |
| n+1 |
点评：本题考查数列的前n项和的求法，是基础题，解题时要注意裂项求和法的合理运用．
练习册系列答案
相关题目
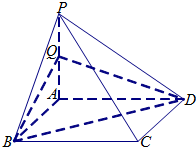如图所示，四棱锥P-ABCD中，底面ABCD是边长为2的正方形，侧棱PA⊥底面ABCD，且PA=2，Q是PA的中点．