题目内容
已知区间[m,n]的长度为n-m(n>m),设集合A=[0,t](t>0),集合B=[a,b](b>a),从集合A到集合B的函数f:x→y=2x+t,若集合B的长度比集合A的长度大5,则实数t= .
考点:函数的值域,函数的定义域及其求法
专题:函数的性质及应用
分析:利用区间长度的概念以及函数的单调性求出t的值即可.
解答:
解:∵集合A的“长度”为t-0=t,
且函数f:x→y=2x+t是单调增函数,
∴集合B的长度为(2t+t)-t=2t
又集合B的长度比集合A的长度大5,
∴2t-t=5,
∴t=5,
即实数t=5.
故答案为:5.
且函数f:x→y=2x+t是单调增函数,
∴集合B的长度为(2t+t)-t=2t
又集合B的长度比集合A的长度大5,
∴2t-t=5,
∴t=5,
即实数t=5.
故答案为:5.
点评:本题考查了新定义的区间长度的计算问题,解题时应先理解新定义的概念,利用概念解答问题,是基础题.

练习册系列答案
相关题目
设复数z满足(z+1)i=-3+2i(i为虚数单位),则z的实部是( )
| A、1 | B、2 | C、3 | D、4 |
双曲线
-
=1的离心率e=2,则双曲线的渐近线方程为( )
| y2 |
| 16 |
| x2 |
| m |
A、y=±
| ||||
B、y=±
| ||||
| C、y=±2x | ||||
D、y=±
|
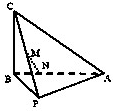 如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.
如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.