题目内容
已知关于x的方程为2kx2-2x-3k-2=0的两个实数根一个小于1,另一个大于1,则实数k的取值范围是( )
| A、k>0 |
| B、k<-4 |
| C、-4<k<0 |
| D、k<-4或k>0 |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:列出
或
即可.
|
|
解答:
解:设f(x)=2kx2-2x-3k-2
∵方程为2kx2-2x-3k-2=0的两个实数根一个小于1,另一个大于1,
∴
或
k>0或k<-4
故选:D
∵方程为2kx2-2x-3k-2=0的两个实数根一个小于1,另一个大于1,
∴
|
|
k>0或k<-4
故选:D
点评:本题考查了函数的图象的运用,解不等式,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
若命题“p∨q”与命题“¬p”都是真命题,则( )
| A、命p不一定是假命题 |
| B、命题q一定是真命题 |
| C、命题q不一定是真命题 |
| D、命题p与命题q同真同假 |
已知y=f(x+
)为偶函数,且当任意
≤x1<x2<+∞时,总有
<0,则下列关系式中一定成立的是( )
| 3 |
| 2 |
| 3 |
| 2 |
| f(x1)-f(x2) |
| x1-x2 |
| A、f(3)<f(1)<f(π) |
| B、f(π)<f(0)<f(1) |
| C、f(0)<f(1)<f(2) |
| D、f(0)<f(π)<f(2) |
设函数f(x)=loga|x|(a>0且a≠1),在(-∞,0)上单调递增,则f(a+1)与f(1)的大小关系为( )
| A、f(a+1)=f(1) |
| B、f(a+1)>f(1) |
| C、f(a+1)<f(1) |
| D、不确定 |
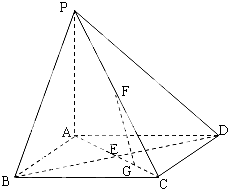 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为EC中点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为EC中点.