题目内容
已知关于x的方程为
+x2=2x+
,则该方程实数解的个数是( )
| 1 |
| |x| |
| 3|x| |
| x |
| A、1 | B、2 | C、3 | D、4 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:分x>0时和当x<0时两种情况,结合反比例函数和二次函数的图象和性质,讨论方程
+x2=2x+
根的个数,综合讨论结果,可得答案.
| 1 |
| |x| |
| 3|x| |
| x |
解答:
解:当x>0时,
方程
+x2=2x+
可化为:
+x2=2x+3,
即
=-x2+2x+3,
由y=
和y=-x2+2x+3的图象在x>0时有两个交点,
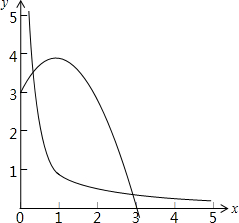
可得当x>0时,
=-x2+2x+3有两个解,即方程
+x2=2x+
有两个解,
当x<0时,
方程
+x2=2x+
可化为:-
+x2=2x-3,
即
=x2-2x+3,
由y=
和y=x2-2x+3的图象在x<0时没有交点,
可得当x<0时,
=x2-2x+3无解,即方程
+x2=2x+
无解,
综上所述方程
+x2=2x+
有2解,
故选:B
方程
| 1 |
| |x| |
| 3|x| |
| x |
| 1 |
| x |
即
| 1 |
| x |
由y=
| 1 |
| x |

可得当x>0时,
| 1 |
| x |
| 1 |
| |x| |
| 3|x| |
| x |
当x<0时,
方程
| 1 |
| |x| |
| 3|x| |
| x |
| 1 |
| x |
即
| 1 |
| x |
由y=
| 1 |
| x |
可得当x<0时,
| 1 |
| x |
| 1 |
| |x| |
| 3|x| |
| x |
综上所述方程
| 1 |
| |x| |
| 3|x| |
| x |
故选:B
点评:本题考查的知识点是根的存在性及个数判断,数形结合思想,分类讨论思想,难度比较大.

练习册系列答案
相关题目
已知圆x2+y2=4与圆x2+y2-2y-6=0,则两圆的公共弦长为( )
A、
| ||
B、2
| ||
| C、2 | ||
| D、1 |
若命题“p∨q”与命题“¬p”都是真命题,则( )
| A、命p不一定是假命题 |
| B、命题q一定是真命题 |
| C、命题q不一定是真命题 |
| D、命题p与命题q同真同假 |
已知y=f(x+
)为偶函数,且当任意
≤x1<x2<+∞时,总有
<0,则下列关系式中一定成立的是( )
| 3 |
| 2 |
| 3 |
| 2 |
| f(x1)-f(x2) |
| x1-x2 |
| A、f(3)<f(1)<f(π) |
| B、f(π)<f(0)<f(1) |
| C、f(0)<f(1)<f(2) |
| D、f(0)<f(π)<f(2) |
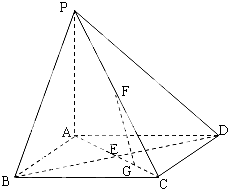 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为EC中点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为EC中点.