题目内容
已知a,b,c∈R,命题“若 a+b+c=1,则a2+b2+c2≤
”的否命题是( )
| 1 |
| 9 |
A、若a2+b2+c2≥1,则a+b+c=
| ||
B、若a+b+c=1,则a2+b2+c2<
| ||
C、若a+b+c≠1,则a2+b2+c2<
| ||
D、若a+b+c≠1,则a2+b2+c2>
|
考点:四种命题
专题:简易逻辑
分析:本题考察命题的否命题,否定原命题的条件做为否命题的条件,原命题的结论否定作为否命题的结论即可.
解答:
解:命题“若 a+b+c=1,则a2+b2+c2≤
”的否命题是“若 a+b+c≠1,则a2+b2+c2>
”,
故选:D.
| 1 |
| 9 |
| 1 |
| 9 |
故选:D.
点评:注意否命题和命题的否定的区分,命题的否定不是四种命题中的任何一种,而且是对整个命题的否定,与原命题真假性相反.

练习册系列答案
相关题目
已知圆x2+y2=4与圆x2+y2-2y-6=0,则两圆的公共弦长为( )
A、
| ||
B、2
| ||
| C、2 | ||
| D、1 |
已知y=f(x+
)为偶函数,且当任意
≤x1<x2<+∞时,总有
<0,则下列关系式中一定成立的是( )
| 3 |
| 2 |
| 3 |
| 2 |
| f(x1)-f(x2) |
| x1-x2 |
| A、f(3)<f(1)<f(π) |
| B、f(π)<f(0)<f(1) |
| C、f(0)<f(1)<f(2) |
| D、f(0)<f(π)<f(2) |
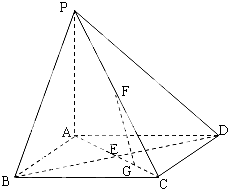 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为EC中点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为EC中点.