题目内容
19.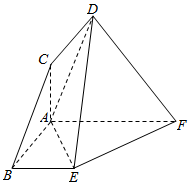 如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.(1)求证:AC⊥平面ABEF;
(2)求三棱锥D-AEF的体积.
分析 (1)在△ABC中使用余弦定理解出AC,利用勾股定理的逆定理得出AC⊥AB,根据面面垂直的性质得出AC⊥平面ABEF;
(2)由CD∥AB可得CD∥平面ABEF,于是VD-AEF=VC-AEF=$\frac{1}{3}{S}_{△AEF}•AC$.
解答 解:(1)在△ABC中,AB=1,BC=2,$∠CBA=\frac{π}{3}$,
由余弦定理得AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BCcos∠CBA}$=$\sqrt{3}$.
∴AB2+AC2=BC2,∴AC⊥AB.
∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,AC?平面ABCD,
∴AC⊥平面ABEF.
(2)∵四边形ABCD是平行四边形,∴CD∥AB,
∵CD?平面ABEF,AB?平面ABEF,
∴CD∥平面ABEF,
∴VD-AEF=VC-AEF=$\frac{1}{3}{S}_{△AEF}•AC$=$\frac{1}{3}×\frac{1}{2}×AF×AB×AC$=$\frac{1}{3}×\frac{1}{2}×1×3×\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查了面面垂直的性质,线面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
7.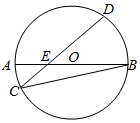 如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )
如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )
 如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )
如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )| A. | 1 | B. | $\frac{3\sqrt{5}}{5}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3\sqrt{7}}{7}$ |
14.一底面是直角梯形的四棱柱的正(主)视图,侧(左)视图如图所示,则该四棱柱的体积为( )
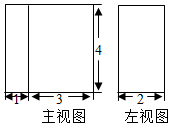

| A. | 20 | B. | 28 | C. | 20或32 | D. | 20或28 |
11.阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为( )
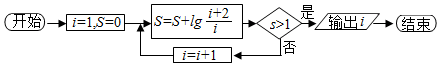
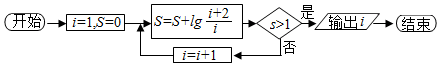
| A. | 4 | B. | 11 | C. | 13 | D. | 15 |
8.函数f(x)是定义在(0,+∞)上的单调函数,且对定义域内的任意x,均有f(f(x)-lnx-x3)=2,则f(e)=( )
| A. | e3+1 | B. | e3+2 | C. | e3+e+1 | D. | e3+e+2 |
9.已知点M是△ABC所在平面内的一点,且满足5$\overrightarrow{AM}$=$\overrightarrow{AB}$+2$\overrightarrow{AC}$,则△AMB与△ABC的面积比为( )
| A. | $\frac{5}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{7}{5}$ | D. | $\frac{5}{7}$ |