题目内容
7.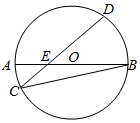 如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )
如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )| A. | 1 | B. | $\frac{3\sqrt{5}}{5}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3\sqrt{7}}{7}$ |
分析 由正弦定理可得$\frac{CE}{sinB}=\frac{3}{\frac{1}{2}}$,CE=6sinB,AC=4sinB,△ACE中,由余弦定理求出sinB,即可求出线段CE的长.
解答  解:连接AC,
解:连接AC,
∵AB是圆O的直径,
∴∠ACB=90°,
∵∠BCD=30°,
∴∠ACE=60°.
由正弦定理可得$\frac{CE}{sinB}=\frac{3}{\frac{1}{2}}$,∴CE=6sinB,
∵AC=4sinB,
∴△ACE中,由余弦定理可得1=(4sinB)2+(6sinB)2-2×4sinB×6sinB×$\frac{1}{2}$,
∴sinB=$\frac{\sqrt{7}}{14}$,
∴CE=6sinB=$\frac{3\sqrt{7}}{7}$.
故选:D.
点评 本题考查正弦定理、余弦定理的运用,考查学生的计算能力,正确求出sinB是解题的关键所在.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.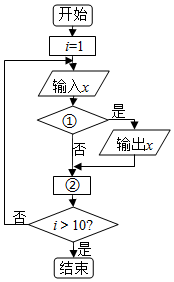 如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
 如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )| A. | x>60?,i=i+1 | B. | x<60?,i=i+1 | C. | x>60?,i=i-1 | D. | x<60?,i=i-1 |
16.执行如图所示的程序框图,若输出的S值为-4,则条件框内应填写( )


| A. | i>3? | B. | i<5? | C. | i>4? | D. | i<4? |
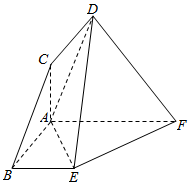 如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.