题目内容
9.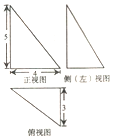 《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )| A. | 200π | B. | 50π | C. | 100π | D. | $\frac{125\sqrt{2}}{3}$π |
分析 几何体复原为底面是直角三角形,一条侧棱垂直底面直角顶点的三棱锥,扩展为长方体,长方体的对角线的长,就是外接球的直径,然后求其的表面积.
解答 解:由三视图复原几何体,几何体是底面是直角三角形,
一条侧棱垂直底面直角顶点的三棱锥;扩展为长方体,也外接与球,
它的对角线的长为球的直径:$\sqrt{9+16+25}$=5$\sqrt{2}$
该三棱锥的外接球的表面积为:$4π•(\frac{5\sqrt{2}}{2})^{2}$=50π,
故选B.
点评 本题考查三视图,几何体的外接球的表面积,考查空间想象能力,计算能力,是基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
19.在学期初,某班开展任课教师对特困生的帮扶活动,已知该班有3名青年任课教师与4名特困生结成帮扶关系,若这3名青年教师每位至少与一名学生结成帮扶关系,又这4名特困学生都能且只能得到一名教师的帮扶,那么不同的帮扶方案的种数为( )
| A. | 36 | B. | 72 | C. | 24 | D. | 48 |
17.若将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位,则平移后的图象( )
| A. | 关于点$(-\frac{π}{12},0)$对称 | B. | 关于直线$x=-\frac{π}{12}$对称 | ||
| C. | 关于点$(\frac{π}{12},0)$对称 | D. | 关于直线$x=\frac{π}{12}$对称 |
14.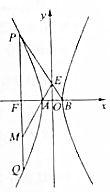 已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )
已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )
 已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )
已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
1.五个人负责一个社团的周一至周五的值班工作,每人一天,则甲同学不值周一,乙同学不值周五,且甲,乙不相邻的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{7}{20}$ | C. | $\frac{2}{5}$ | D. | $\frac{13}{30}$ |
18.已知集合$M=\{x|\frac{2x-1}{x+1}≤1\}$,N={x|-1<x<1},则( )
| A. | M?N | B. | N?M | C. | M=N | D. | M∩N=∅ |
19.设集合$A=[(x,y)|\frac{x^2}{25}+\frac{y^2}{16}≤1],B=[(x,y)|\left\{\begin{array}{l}|x|≤m\\|y|≤n\end{array}\right.,0<m<5,0<n<4且(m,n)∈A]$,则集合∁AB对应图形面积取得最小值时,m+n的值为( )
| A. | $\frac{{9\sqrt{2}}}{2}$ | B. | $5\sqrt{2}$ | C. | 6 | D. | 8 |
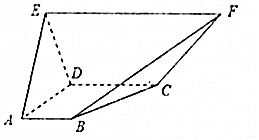 在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.
在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.