题目内容
1.五个人负责一个社团的周一至周五的值班工作,每人一天,则甲同学不值周一,乙同学不值周五,且甲,乙不相邻的概率是( )| A. | $\frac{3}{10}$ | B. | $\frac{7}{20}$ | C. | $\frac{2}{5}$ | D. | $\frac{13}{30}$ |
分析 基本事件总数n=${A}_{5}^{5}=120$,甲同学不值周一,乙同学不值周五,且甲,乙不相邻,甲乙排列有3种情况:①乙在周一,甲不在周五,乙x甲xx,乙不在周一,甲在周五,x乙xx甲,③乙不在周一,甲不在周五,x乙x甲x,由此求出甲同学不值周一,乙同学不值周五,且甲,乙不相邻包含贩基本事件个数,由此能求出结果.
解答 解:五个人负责一个社团的周一至周五的值班工作,每人一天,
基本事件总数n=${A}_{5}^{5}=120$,
甲同学不值周一,乙同学不值周五,
由题意得,甲不在周一,乙不在周五,且甲,乙不相邻,甲乙排列有3种情况:
①乙在周一,甲不在周五,乙x甲xx,排列数:${A}_{4}^{4}-{A}_{3}^{3}$=18,
②乙不在周一,甲在周五,x乙xx甲,排列数:${A}_{2}^{1}{A}_{3}^{3}$=12,
③乙不在周一,甲不在周五,x乙x甲x,排列数:${A}_{3}^{3}{A}_{2}^{2}$=12,
共有18+12+12=42,
∴甲同学不值周一,乙同学不值周五,且甲,乙不相邻的概率P=$\frac{42}{120}=\frac{7}{20}$.
故选:B.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.四个大学生分到两个单位,每个单位至少分一个的分配方案有( )
| A. | 10种 | B. | 14种 | C. | 20种 | D. | 24种 |
12.某公司准备将1000万元资金投入到市环保工程建设中,现有甲、乙两个建设项目选择,若投资甲项目一年后可获得的利润ξ1(万元)的概率分布列如表所示:
且ξ1的期望E(ξ1)=120;若投资乙项目一年后可获得的利润ξ2(万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为p(0<p<1)和1-p.若乙项目产品价格一年内调整次数X(次数)与ξ2的关系如表所示:
(Ⅰ)求m,n的值;
(Ⅱ)求ξ2的分布列;
(Ⅲ)若该公司投资乙项目一年后能获得较多的利润,求p的取值范围.
| ξ1 | 110 | 120 | 170 |
| P | m | 0.4 | n |
| X | 0 | 1 | 2 |
| ξ2 | 41.2 | 117.6 | 204.0 |
(Ⅱ)求ξ2的分布列;
(Ⅲ)若该公司投资乙项目一年后能获得较多的利润,求p的取值范围.
9.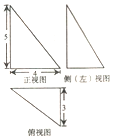 《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
 《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )| A. | 200π | B. | 50π | C. | 100π | D. | $\frac{125\sqrt{2}}{3}$π |
13.设F(c,0)是双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点,$P(\frac{a^2}{c},\frac{{\sqrt{2}a}}{2})$为直线上一点,且直线垂直于x轴,垂足为M,若△PMF等腰三角形,则E的离心率为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
10.某经销商试销A、B两种商品一个月(30天)的记录如下:
若售出每种商品1件均获利40元,用X,Y表示售出A、B商品的日利润值(单位:元).将频率视为概率.
(1)设两种商品的销售量互不影响,求两种商品日获利值均超过100元的概率;
(2)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由.
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 3 | 5 | 7 | 7 | 5 | 3 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
(1)设两种商品的销售量互不影响,求两种商品日获利值均超过100元的概率;
(2)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由.
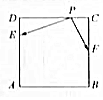 如图,正方形ABCD的边长为8,点E,F分别在边AD,BC上,且AE=3ED,CF=FB,如果对于常数m,在正方形ABC的四条边上有且只有6个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=m成立,那么m的取值范围是(-1,8).
如图,正方形ABCD的边长为8,点E,F分别在边AD,BC上,且AE=3ED,CF=FB,如果对于常数m,在正方形ABC的四条边上有且只有6个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=m成立,那么m的取值范围是(-1,8).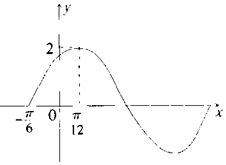 已知函数f(x)=Asin($ωx+ϕ),(ω>0,A>0,ϕ∈(0,\frac{π}{2}))$部分图象如图所示.
已知函数f(x)=Asin($ωx+ϕ),(ω>0,A>0,ϕ∈(0,\frac{π}{2}))$部分图象如图所示.