题目内容
4.已知等差数列{an}的前n项和为Sn,且满足S4=24,S7=63.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=2an+an,求数列{bn}的前n项和Tn.
分析 (I)利用等差数列的通项公式与求和公式即可得出.
(II)bn=2an+an=2×4n+(2n+1),再利用等差数列与等比数列的求和公式即可得出.
解答 解:(Ⅰ)∵{an}为等差数列,
∴$\left\{\begin{array}{l}{S_4}=4{a_1}+\frac{4×3}{2}d=24\\{S_7}=7{a_1}+\frac{7×6}{2}d=63\end{array}\right.$$⇒\left\{\begin{array}{l}{a_1}=3\\ d=2\end{array}\right.⇒{a_n}=2n+1$.
(Ⅱ)∵${b_n}={2^{a_n}}+{a_n}={2^{2n+1}}+(2n+1)$=2×4n+(2n+1),
∴${T_n}=2(4+{4^2}+…+{4^n})$+(3+5+…+2n+1)=$2×\frac{{4(1-{4^n})}}{1-4}+\frac{n(3+2n+1)}{2}$=$\frac{8}{3}({4^n}-1)+{n^2}+2n$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.从5种主料职工选2种,8种辅料中选3种烹制菜肴,烹制方式有5种,那么最多可以烹制出不同的菜肴种数为( )
| A. | 18 | B. | 200 | C. | 2800 | D. | 33600 |
12.某公司准备将1000万元资金投入到市环保工程建设中,现有甲、乙两个建设项目选择,若投资甲项目一年后可获得的利润ξ1(万元)的概率分布列如表所示:
且ξ1的期望E(ξ1)=120;若投资乙项目一年后可获得的利润ξ2(万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为p(0<p<1)和1-p.若乙项目产品价格一年内调整次数X(次数)与ξ2的关系如表所示:
(Ⅰ)求m,n的值;
(Ⅱ)求ξ2的分布列;
(Ⅲ)若该公司投资乙项目一年后能获得较多的利润,求p的取值范围.
| ξ1 | 110 | 120 | 170 |
| P | m | 0.4 | n |
| X | 0 | 1 | 2 |
| ξ2 | 41.2 | 117.6 | 204.0 |
(Ⅱ)求ξ2的分布列;
(Ⅲ)若该公司投资乙项目一年后能获得较多的利润,求p的取值范围.
19.从区间[-2,2]中随机选取一个实数a,则函数f(x)=4x-a•2x+1+1有零点的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
9.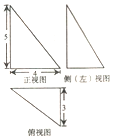 《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
 《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )| A. | 200π | B. | 50π | C. | 100π | D. | $\frac{125\sqrt{2}}{3}$π |
13.设F(c,0)是双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点,$P(\frac{a^2}{c},\frac{{\sqrt{2}a}}{2})$为直线上一点,且直线垂直于x轴,垂足为M,若△PMF等腰三角形,则E的离心率为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
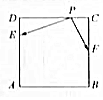 如图,正方形ABCD的边长为8,点E,F分别在边AD,BC上,且AE=3ED,CF=FB,如果对于常数m,在正方形ABC的四条边上有且只有6个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=m成立,那么m的取值范围是(-1,8).
如图,正方形ABCD的边长为8,点E,F分别在边AD,BC上,且AE=3ED,CF=FB,如果对于常数m,在正方形ABC的四条边上有且只有6个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=m成立,那么m的取值范围是(-1,8).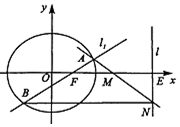 已知椭圆$E:\frac{x^2}{5}+\frac{y^2}{4}=1$的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.
已知椭圆$E:\frac{x^2}{5}+\frac{y^2}{4}=1$的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.