题目内容
已知一个几何体的三视图如图所示，根据图中尺寸可得该几何体的表面积为（ ）
| A、26 | ||
B、24+4
| ||
C、28+
| ||
D、26+2
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可知：该几何体是正方体和一个三棱锥的组合体，分别求出各个面的面积，相加可得答案．
解答：
解：由已知中的三视图可知：该几何体是正方体和一个三棱锥的组合体，
其直观图如下图所示：
由图可知：该几何体的表面共有9个面，其中：
边长为2的正方形有5个，直角边长为2的等腰直角三角形有三个，边长为2
的等边三角形1个，
故表面积S=5（2×2）+3×（
×2×2）+
×(2
)2=26+2
，
故选：D
其直观图如下图所示：
由图可知：该几何体的表面共有9个面，其中：
边长为2的正方形有5个，直角边长为2的等腰直角三角形有三个，边长为2
| 2 |
故表面积S=5（2×2）+3×（
| 1 |
| 2 |
| ||
| 4 |
| 2 |
| 3 |
故选：D
点评：本题考查的知识点是由三视图求表面积，其中分析出几何体的形状是解答的关键．
练习册系列答案
相关题目
在复平面内，复数
（其中i为虚数单位）对应的点位于（ ）
| ||
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设直线l⊥平面α，直线m?平面β，则（ ）
| A、若m∥α，则l∥m |
| B、若α∥β，则l⊥m |
| C、若l⊥m，则α∥β |
| D、若α⊥β，则l∥m |
读程序：
S=0
sum=0
for i=1 to 100
S=S+i
i=i+1
sum=sum+S
next
输出sum
该程序的运行结果是（ ）的值．
S=0
sum=0
for i=1 to 100
S=S+i
i=i+1
sum=sum+S
next
输出sum
该程序的运行结果是（ ）的值．
| A、1+2+3+…+99 |
| B、1+2+3+…+100 |
| C、1+（1+2）+（1+2+3）+…+（1+2+3+…+99） |
| D、1+（1+2）+（1+2+3）+…+（1+2+3+…+100） |
设某种动物从出生算起活20岁以上的概率为0.9，活到25岁以上的概率为0.5，现有一个20岁的这种动物，则它能活到25岁以上的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，已知a=3，c=3
，A=30°，则角C等于（ ）
| 3 |
| A、30° | B、60°或120° |
| C、60° | D、120° |
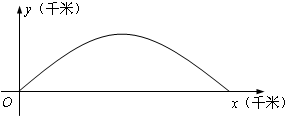如图，建立平面直角坐标系xOy，x轴在地平面上，y轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程y=kx-