题目内容
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R),则直线l和圆C的交点个数为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:由条件求得直线l经过定点A(3,1),且A在圆的内部,可得直线l和圆C相交.
解答:
解:直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R),即 (x+y-4)+m(2x+y-7)=0,
由
求得
,可得直线l经过定点A(3,1).
再根据AC=
=
,小于半径,可得点A在圆C的内部,故直线l和圆C相交,
故答案为:2.
由
|
|
再根据AC=
| 4+1 |
| 5 |
故答案为:2.
点评:本题主要考查直线经过定点问题,直线和圆的位置关系的判定,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
空间四边形ABCD中,若AD⊥BC,AD⊥BD,那么有( )
| A、平面ABC⊥平面ADC |
| B、平面ABC⊥平面ADB |
| C、平面ABC⊥平面DBC |
| D、平面ADC⊥平面DBC |
已知一个三棱柱的三视图如图所示,则该三棱柱的表面积为( )
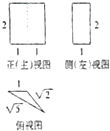

A、4
| ||||||
B、2
| ||||||
C、
| ||||||
D、2
|
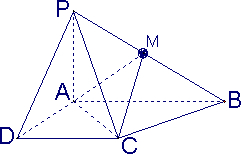 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=