题目内容
15．
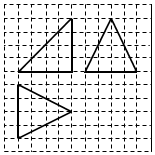如图，网络纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的各个面的面积中，最小的值为（ ）| A． | 2$\sqrt{5}$ | B． | 8 | C． | 4$\sqrt{5}$ | D． | 8$\sqrt{2}$ |
分析 由三视图知该几何体为是三棱锥，由三视图判断出线面的位置关系、并求出棱长，判断出几何体的各个面的面积最小的面，并求出此面的面积．
解答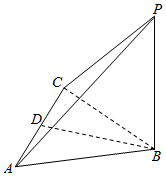 
解：根据三视图可知几何体是一个三棱锥且PB⊥平面ABC，
底面是一个等腰三角形，且D是底边AC的中点，
由三视图得：PB=AC=4，高BD=4，
∴AB=BC=$\sqrt{{2}^{2}+{4}^{2}}$=$2\sqrt{5}$＞4，
∵PB⊥BC，PB⊥AB，∴PC＞BC，PA＞AB，
∴几何体的各个面的面积中最小的是△ABC，
△ABC的面积S=$\frac{1}{2}×4×4$=8
故选：B．
点评 本题考查由三视图求几何体的表面积，线面垂直的定义以及勾股定理，考查空间想象能力，三视图正确复原几何体是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
3．设函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}，x≤1}\\{lo{g}_{2}x，x＞1}\end{array}\right.$，若f（a）＞1，则a的取值范围是（ ）
| A． | （-∞，1）∪（2，+∞） | B． | （0，+∞） | C． | （2，+∞） | D． | （-∞，0）∪（2，+∞） |
20．设f（x）是定义在R上的函数，对x∈R都有f（-x）=f（x），f（2+x）=f（2-x），且当x∈[-2，0]时，f（x）=（$\frac{1}{2}$）x-1，若在区间（-2，6]内关于x的方程f（x）-loga（x+2）=0（a＞1）恰有3个不同的实数根，则a的取值范围是（ ）
| A． | （1，2） | B． | （2，+∞） | C． | （1，$\root{3}{4}$） | D． | （$\root{3}{4}$，2） |
7．若函数f（x）满足：?x∈R，f（2x）=sinx+f（x），且f（1）=1，则（ ）
| A． | f（$\frac{1}{{2}^{2016}}$）＜$\frac{1}{{2}^{2016}}$ | B． | f（$\frac{1}{{2}^{2015}}$）＜$\frac{1}{{2}^{2016}}$ | ||
| C． | f（$\frac{1}{{2}^{2014}}$）＜$\frac{1}{4}$+$\frac{3}{{2}^{2016}}$ | D． | f（$\frac{1}{{2}^{2013}}$）＞$\frac{1}{4}$+$\frac{3}{{2}^{2015}}$ |
4．
已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜π），若对满足|f（x1）-f（x2）|=2的x1，x2有|x1-x2|min=π，且函数f（x）的部分图象如图，则函数f（x）的解析式为（ ）
已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜π），若对满足|f（x1）-f（x2）|=2的x1，x2有|x1-x2|min=π，且函数f（x）的部分图象如图，则函数f（x）的解析式为（ ）| A． | f（x）=sin（x+$\frac{5π}{6}$） | B． | f（x）=sin（x-$\frac{π}{6}$） | C． | f（x）=sin（2x+$\frac{2π}{3}$） | D． | f（x）=sin（2x-$\frac{π}{3}$） |
5．
执行如图所示的程序框图，如果输入n的值为4，则输出的S的值为（ ）
执行如图所示的程序框图，如果输入n的值为4，则输出的S的值为（ ）| A． | 15 | B． | 6 | C． | -10 | D． | -21 |