题目内容
4. 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π),若对满足|f(x1)-f(x2)|=2的x1,x2有|x1-x2|min=π,且函数f(x)的部分图象如图,则函数f(x)的解析式为( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π),若对满足|f(x1)-f(x2)|=2的x1,x2有|x1-x2|min=π,且函数f(x)的部分图象如图,则函数f(x)的解析式为( )| A. | f(x)=sin(x+$\frac{5π}{6}$) | B. | f(x)=sin(x-$\frac{π}{6}$) | C. | f(x)=sin(2x+$\frac{2π}{3}$) | D. | f(x)=sin(2x-$\frac{π}{3}$) |
分析 由题意可得函数的周期为2π,可得ω=1,代入点($\frac{π}{6}$,0)结合角的范围可得φ值,再结合图象验证可得.
解答 解:∵对满足|f(x1)-f(x2)|=2的x1,x2有|x1-x2|min=π,
∴函数的周期为2π,故$\frac{2π}{ω}$=2π,解得ω=1,故f(x)=sin(x+φ),
又函数图象过点($\frac{π}{6}$,0),故sin($\frac{π}{6}$+φ)=0,
结合|φ|<π可得φ=$\frac{5π}{6}$或φ=-$\frac{π}{6}$,
当φ=-$\frac{π}{6}$时,函数解析式为f(x)=sin(x-$\frac{π}{6}$),
当x=0时,f(0)=sin(-$\frac{π}{6}$)<0,这与函数图象矛盾,应舍去
故选:A.
点评 本题考查正弦函数的图象,涉及函数的周期性和特殊点,属基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
15.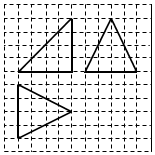 如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )
如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )
 如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )
如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )| A. | 2$\sqrt{5}$ | B. | 8 | C. | 4$\sqrt{5}$ | D. | 8$\sqrt{2}$ |
12.已知sin($\frac{3π}{2}$+α)=$\frac{3}{5}$,则sin($\frac{π}{2}$+2α)=( )
| A. | $\frac{7}{25}$ | B. | -$\frac{7}{25}$ | C. | $\frac{24}{25}$ | D. | -$\frac{24}{25}$ |
16.已知复数i•(1+ai)为纯虚数,那么实数a的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |