题目内容
5.定义在[-1,1]上的函数y=f(x)是增函数且是奇函数,若f(-a+1)+f(4a-5)>0.求实数a的取值范围.分析 根据函数奇偶性和单调性的关系将不等式进行转化求解即可.
解答 解:由f(-a+1)+f(4a-5)>0得f(4a-5)>-f(-a+1),
∵定义在[-1,1]上的函数y=f(x)是增函数且是奇函数,
∴不等式等价为f(4a-5)>f(a-1),
则满足$\left\{\begin{array}{l}{-1≤4a-5≤1}\\{-1≤a-1≤1}\\{4a-5>a-1}\end{array}\right.$,
得$\left\{\begin{array}{l}{1≤a≤\frac{3}{2}}\\{0≤a≤2}\\{a>\frac{4}{3}}\end{array}\right.$,即$\frac{4}{3}$<a≤$\frac{3}{2}$,
即实数a的取值范围是$\frac{4}{3}$<a≤$\frac{3}{2}$.
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性的关系将不等式进行转化是解决本题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
13.已知非零向量$\overrightarrow a$、$\overrightarrow b$满足$\left|{\overrightarrow a+\overrightarrow b}\right|=\left|{\overrightarrow a-\overrightarrow b}\right|=\frac{{2\sqrt{3}}}{3}\left|{\overrightarrow a}\right|$,则$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$的夹角为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
20.已知直线l的倾斜角为α,且60°<α≤135°,则直线l斜率的取值范围是( )
| A. | $(\sqrt{3},+∞)$ | B. | $[-1,\sqrt{3})$ | C. | $(-∞,-1]∪(\sqrt{3},+∞)$ | D. | $(-∞,-1)∪[\sqrt{3},+∞)$ |
17.已知函数$f(x)=3sin(ωx-\frac{π}{4})(ω>0)$,函数相邻两个零点之差的绝对值为$\frac{π}{2}$,则函数f(x)图象的对称轴方程可以是( )
| A. | $x=\frac{π}{8}$ | B. | $x=-\frac{π}{8}$ | C. | $x=\frac{5π}{8}$ | D. | $x=-\frac{π}{4}$ |
15.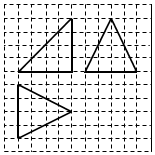 如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )
如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )
 如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )
如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )| A. | 2$\sqrt{5}$ | B. | 8 | C. | 4$\sqrt{5}$ | D. | 8$\sqrt{2}$ |
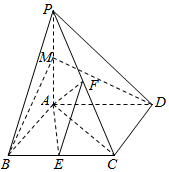 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,直线PC与底面ABCD所成的角45°,E,F,M分别是BC,PC,PA的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,直线PC与底面ABCD所成的角45°,E,F,M分别是BC,PC,PA的中点.