题目内容
10.讨论函数f(x)=$\underset{lim}{n→∞}$$\frac{x+{x}^{3}{e}^{nx}}{x+{e}^{nx}}$的连续性(n为正整数).分析 利用函数连续的定义即可判断出结论.
解答 解:当x=0时,f(0)=0,
x≠0时,f(x)=$\underset{lim}{n→∞}$$\frac{x+{x}^{3}{e}^{nx}}{x+{e}^{nx}}$=$\underset{lim}{n→∞}$$\frac{\frac{x}{{e}^{nx}}+{x}^{3}}{\frac{x}{{e}^{nx}}+1}$=x3,∴x→0时,f(x)→0,
因此函数f(x)在x=0处连续.
x≠0时,函数f(x)连续.
因此函数x∈R时连续.
点评 本题考查了函数连续的定义、极限的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知直线l的倾斜角为α,且60°<α≤135°,则直线l斜率的取值范围是( )
| A. | $(\sqrt{3},+∞)$ | B. | $[-1,\sqrt{3})$ | C. | $(-∞,-1]∪(\sqrt{3},+∞)$ | D. | $(-∞,-1)∪[\sqrt{3},+∞)$ |
15.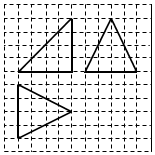 如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )
如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )
 如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )
如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的各个面的面积中,最小的值为( )| A. | 2$\sqrt{5}$ | B. | 8 | C. | 4$\sqrt{5}$ | D. | 8$\sqrt{2}$ |
2.执行如图的程序框图,若输入n=3,则输出的S=( )
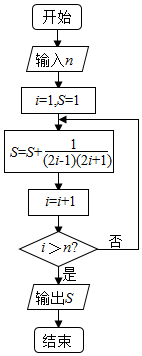

| A. | $\frac{3}{7}$ | B. | $\frac{8}{7}$ | C. | $\frac{10}{7}$ | D. | $\frac{13}{7}$ |
20.根据我国发布的《环境空气质量指数AQI技术规定》:空气质量指数划分为0~50,51~100,101~150,151~200,201~300和大于300六级,对应于空气质量指数的六个级别,指数越大,级别越高,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数小于150时,可以户外运动;空气质量指数151及以上,不适合进行旅游等户外运动,以下是我市2013年3月中旬的空气质量指数情况:
(1)求3月份市民不适合进行户外活动的概率?
(2)一外地游客在3月份来我市旅游,想连续游玩两天,求适合旅游的概率.
| 时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
| AQ1 | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
(2)一外地游客在3月份来我市旅游,想连续游玩两天,求适合旅游的概率.