题目内容
3．设函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}，x≤1}\\{lo{g}_{2}x，x＞1}\end{array}\right.$，若f（a）＞1，则a的取值范围是（ ）| A． | （-∞，1）∪（2，+∞） | B． | （0，+∞） | C． | （2，+∞） | D． | （-∞，0）∪（2，+∞） |
分析 根据分段函数的表达式，分别对a进行分类讨论即可得到结论．
解答 解：若a＞1，由f（a）＞1得l0g2a＞1，即a＞2，此时a＞2，
若a≤1，则由f（a）＞11得2-a＞1，则-a＞0，即a＜0，此时a＜0
综上a＞2或a＜0，
即a的取值范围是（-∞，0）∪（2，+∞），
故选：D
点评 本题主要考查不等式的求解，根据分段函数的表达式，对x进行分类讨论是解决本题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
13．已知非零向量$\overrightarrow a$、$\overrightarrow b$满足$\left|{\overrightarrow a+\overrightarrow b}\right|=\left|{\overrightarrow a-\overrightarrow b}\right|=\frac{{2\sqrt{3}}}{3}\left|{\overrightarrow a}\right|$，则$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$的夹角为（ ）
| A． | $\frac{5π}{6}$ | B． | $\frac{π}{6}$ | C． | $\frac{2π}{3}$ | D． | $\frac{π}{3}$ |
如图，在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠BCD=120°，四边形BFED为矩形，平面BFED⊥平面ABCD，BF=1
15．
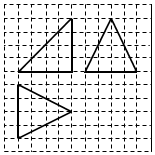如图，网络纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的各个面的面积中，最小的值为（ ）
如图，网络纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的各个面的面积中，最小的值为（ ）| A． | 2$\sqrt{5}$ | B． | 8 | C． | 4$\sqrt{5}$ | D． | 8$\sqrt{2}$ |
12．已知sin（$\frac{3π}{2}$+α）=$\frac{3}{5}$，则sin（$\frac{π}{2}$+2α）=（ ）
| A． | $\frac{7}{25}$ | B． | -$\frac{7}{25}$ | C． | $\frac{24}{25}$ | D． | -$\frac{24}{25}$ |