题目内容

9．已知复数z=$\frac{i}{1+i}$，其中i为虚数单位，则|z|=（　　）
A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\sqrt{2}$D．2

分析 直接由复数代数形式的乘除运算化简复数z，再利用复数求模公式计算得答案．

解答 解：z=$\frac{i}{1+i}$=$\frac{i（1-i）}{（1+i）（1-i）}=\frac{1+i}{2}=\frac{1}{2}+\frac{1}{2}i$，
则|z|=$\sqrt{（\frac{1}{2}）^{2}+（\frac{1}{2}）^{2}}=\frac{\sqrt{2}}{2}$．
故选：B．

点评 本题考查了复数代数形式的乘除运算，考查了复数模的求法，是基础题．

练习册系列答案
相关题目
19．在正方体A1B1C1D1-ABCD中，给出以下命题：
①平面A1BD∥平面D1B1C；
②存在无数条直线，它与该正方体的六个表面所在平面所成的角都相等；
③不存在平面，与该正方体的六个表面所在平面所成的锐二面角的大小都相等；
④AD1与平面A1BD所成角的正弦值为$\frac{{\sqrt{6}}}{3}$．
其中真命题的个数为（　　）
A．1B．2C．3D．4
20．抛物线C：y2=2px（p＞0）的焦点为F，A是C上一点，若A到F的距离是A到y轴距离的两倍，且三角形OAF的面积为1（O为坐标原点），则p的值为（　　）
A．1B．2C．3D．4
17．在△ABC中，“A＜B＜C”是“cos2A＞cos2B＞cos2C”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
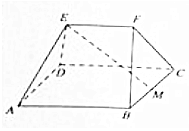4．如图，在多面体ABCDEF中，四边形ABCD为边长为4的正方形，M是BC的中点，EF∥平面ABCD，且EF=2，AE=DE=BF=CF=$2\sqrt{2}$．
（1）求证：ME⊥平面ADE；
（2）求二面角B-AE-D的余弦值．
14．若直角坐标平面内的两点P，Q满足条件：①P，Q都在函数y=f（x）的图象上；②P，Q关于原点对称，则称点对（P，Q）是函数y=f（x）的一对“友好点对”（点对（P，Q）与（Q，P）看作同一对“友好点对”）．已知函数f（x）=$\left\{\begin{array}{l}{{（\frac{1}{2}）}^{x}，x＞0}\\{x+1，x≤0}\end{array}\right.$，则此函数的“友好点对”有（　　）
A．3对B．2对C．1对D．0对
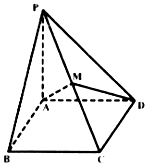1．已知四棱锥P-ABCD中，底面为矩形，PA⊥底面ABCD，PA=BC=1，AB=2，M为PC中点．
（Ⅰ）在图中作出平面ADM与PB的交点N，并指出点N所在位置（不要求给出理由）；
（Ⅱ）在线段CD上是否存在一点E，使得直线AE与平面ADM所成角的正弦值为$\frac{\sqrt{10}}{10}$，若存在，请说明点E的位置；若不存在，请说明理由；
（Ⅲ）求二面角A-MD-C的余弦值．
7．定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M，都有f（x）≤M成立，则称f（x）是D上的确界函数，其中M称为函数f（x）的上确界，已知函数f（x）=1-3•2x+a•4x．
（1）当a=1时，求函数f（x）在（0，+∞）上的值域，并判断函数f（x）在（0，+∞）上是否为确界函数，请说明理由；
（2）若函数f（x）在（-∞，0]上是以4为上确界的确界函数，求实数a的取值范围．
8．执行如图程序框图，若输入的x=2，n=2，依次输入的a为2，2，5，则输出的s=（　　）
A．7B．12C．17D．34

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网