题目内容
11.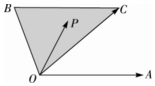 已知图中∠AOC+2∠BOC=π,|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|,BC∥OA,P为图中的阴影中(含边界)任意点,并且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$,下列正确的是①③⑤
已知图中∠AOC+2∠BOC=π,|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|,BC∥OA,P为图中的阴影中(含边界)任意点,并且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OC}$,下列正确的是①③⑤①0≤x+y≤1;
②|x|+|y|≤x2+y2;
③x2+y2≤2;
④存在无数个点P,使得x=-1;
⑤存在无数个点P,使得y=1.
分析 本题考查的知识点是平面向量的基本定理和平行四边形法则,可以将四个答案一一代入,判断点的位置,排除错误答案,即可得到结论.
解答 解:当点P在OB上时|x|=|y|,x+y=0,当点P在△OBC内时,上时|x|<|y|,x+y>0,
当点P在线段BC上时,y=1,-x∈[0,1]
∴①③正确,
对于②,x=1,y∈(0,1)时,②|x|+|y|>x2+y2,故错,
对于④,如图4,∵|$\overrightarrow{OA}$|=|$\overrightarrow{OC}$|,BC∥OA,∴只存在一个点P(B处),使x=-1,故错;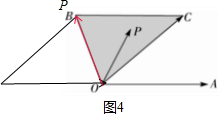
对于⑤,如图5,点P可以是线段BC上任意一点,都使y=1,故⑤正确.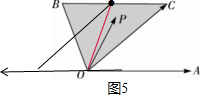
故答案为:①③⑤
点评 本题主要考查平面向量的应用,利用向量的基本定理是解决本题的关键.属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
2.若变量x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≤0}\\{x-3y+3≤0}\end{array}\right.$,则z=($\frac{1}{2}$)4x+8y的最小值为( )
| A. | ($\frac{1}{2}$)28 | B. | ($\frac{1}{2}$)23 | C. | 4 | D. | 1 |
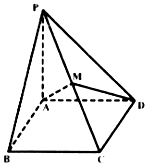 已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.
已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.