题目内容
14.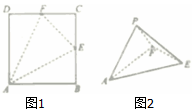 如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )
如图1,ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球面上,则该球的表面积是( )| A. | $\sqrt{6}π$ | B. | 6π | C. | $4\sqrt{3}π$ | D. | 12π |
分析 由已知得PA、PF、PE两两垂直,且PA=2,PE=PF=1,以PA、PE、PF为棱构造一个长方体,则四面体PAEF的四个顶点在这个长方体的外接球上,由此能求出该球的表面积.
解答 解:∵ABCD是边长为2的正方形,点E,F分别为BC,CD的中点,
将△ABE,△ECF,△FDA分别沿AE,EF,FA折起,使B,C,D三点重合于点P,
∴PA、PF、PE两两垂直,且PA=2,PE=PF=1,
以PA、PE、PF为棱构造一个长方体,
则四面体PAEF的四个顶点在这个长方体的外接球上,
∴这个球的半径为R=$\frac{\sqrt{1+1+4}}{2}$=$\frac{\sqrt{6}}{2}$,
∴该球的表面积是S=4πR2=4π×$\frac{6}{4}$=6π.
故选:B.
点评 本题考查球的表面积的求法,是中档题,解题时要认真审题,注意球、四面体的性质及构造法的合理应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若变量x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≤0}\\{x-3y+3≤0}\end{array}\right.$,则z=($\frac{1}{2}$)4x+8y的最小值为( )
| A. | ($\frac{1}{2}$)28 | B. | ($\frac{1}{2}$)23 | C. | 4 | D. | 1 |
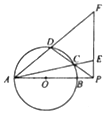 如图,AB是圆O的直径,P是线段AB延长线上一点,割线PCD交圆O于点C,D,过点P作AP的垂线,交线段AC的延长线于点E,交线段AD的延长线于点F,且PE•PF=5,PB=$\frac{1}{2}$OA.
如图,AB是圆O的直径,P是线段AB延长线上一点,割线PCD交圆O于点C,D,过点P作AP的垂线,交线段AC的延长线于点E,交线段AD的延长线于点F,且PE•PF=5,PB=$\frac{1}{2}$OA.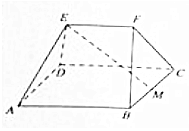 如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.
如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.