题目内容
9.已知e为自然对数的底数,若方程|xlnx-ex+e|=mx在区间[$\frac{1}{e}$,e2]上有三个不同实数根,则实数m的取值范围是[e-$\frac{1}{e}$-2,e-2).分析 令f(x)=xlnx-ex+e,判断f(x)的单调性得出y=|f(x)|在[$\frac{1}{e}$,e2]上的图象,根据图象有3个交点求出m的临界值即可得出m的范围.
解答 解:令f(x)=xlnx-ex+e,则f′(x)=lnx-e+1,
∴当x∈($\frac{1}{e}$,ee-1)时,f′(x)<0,当x∈(ee-1,e2)时,f′(x)>0,
∴f(x)在($\frac{1}{e}$,ee-1)上单调递减,在(ee-1,e2)上单调递增,
又f(1)=0,f(e2)=2e2-e3+e=e(2e+1-e2)<0,
∴|f(x)|=$\left\{\begin{array}{l}{xlnx-ex+e,\frac{1}{e}≤x≤1}\\{-xlnx+ex-e,1<x≤{e}^{2}}\end{array}\right.$,
∴y=|f(x)|的函数图象如图所示:
∵方程|xlnx-ex+e|=mx在区间[$\frac{1}{e}$,e2]上有三个不同实数根,
∴y=mx与y=|f(x)|的图象有3个交点,
设y=m1x经过点(e2,|f(e2)|),则m1=$\frac{e({e}^{2}-2e-1)}{{e}^{2}}$=$e-\frac{1}{e}-2$,
设y=m2x与y=|f(x)|相切,切点为x0,y0,显然1<x0<e2,
则$\left\{\begin{array}{l}{{m}_{2}=-ln{x}_{0}-1+e}\\{{y}_{0}={m}_{2}{x}_{0}}\\{{y}_{0}=-{x}_{0}ln{x}_{0}+e{x}_{0}-e}\end{array}\right.$,解得x0=e,y0=e2-2e,m2=e-2,
∴e-$\frac{1}{e}-2$≤m<e-2.
故答案为[e-$\frac{1}{e}-2$,e-2).
点评 本题考查了函数单调性判断,函数零点个数与函数图象的关系,属于中档题.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
表1 映射f对应法则
| 原像 | 1 | 2 | 3 | 4 |
| 像 | 3 | 4 | 2 | 1 |
| 原像 | 1 | 2 | 3 |
| 像 | 4 | 3 | 1 |
| A. | g[f(3)] | B. | g[f(2)] | C. | g[f(4)] | D. | g[f(1)] |
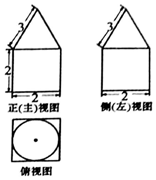
| A. | 4+2$\sqrt{2}$π | B. | 8+2$\sqrt{2}$π | C. | 4+$\frac{2\sqrt{2}}{3}$π | D. | 8+$\frac{2\sqrt{2}}{3}$π |