题目内容
直线l:y=x与园x2+y2-2x-6y=0相交A、B两点,则|AB|= .
考点:直线与圆的位置关系
专题:直线与圆
分析:利用直线与圆的位置关系,得到弦心距、半径与半弦长的关系,解直角三角形求弦长.
解答:
解:因为直线l:y=x与园x2+y2-2x-6y=0相交A、B两点,
并且圆心为(1,3),半径为
,
所以弦心距为圆心到直线l的距离为
=
,
所以
AB=
=2
,
所以AB=4
;
故答案为:4
.
并且圆心为(1,3),半径为
| 10 |
所以弦心距为圆心到直线l的距离为
| |1-3| | ||
|
| 2 |
所以
| 1 |
| 2 |
(
|
| 2 |
所以AB=4
| 2 |
故答案为:4
| 2 |
点评:本题考查了通过直线与圆的位置关系求弦心距、半径或者弦长,经常考查,属于基础题.

练习册系列答案
相关题目
设集合U={1,2,3,4,5},A={1,2,3},B={2,5},则(∁UA)∩(∁UB)=( )
| A、{2} | B、{2,3} |
| C、{4} | D、{1,3} |
实数x、y满足不等式组
,且z=ax+y(a>0)取最小值的最优解有无穷多个,则实数a的取值是( )
|
A、-
| ||
| B、1 | ||
| C、2 | ||
| D、无法确定 |
下列说法中正确的是( )
| A、频率是概率的近似值,随着试验次数增加,频率会越来越接近概率 |
| B、要从1002名学生中用系统抽样的方法选取一个容量为20的样本,需要剔除2名学生,这样对被剔除者不公平 |
| C、用秦九韶算法计算多项式f(x)=12+35x+9x3+5x5+3x6在当x=-1时的值时要用到6次加法和15次乘法 |
| D、数据2,3,4,5的方差是数据4,6,8,10的方差的一半 |
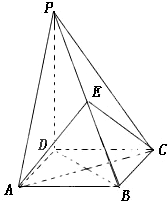 如图,四棱锥P--ABCD的底面是正方形,PD⊥底面ABCD,点E为PB的中点.且PD=
如图,四棱锥P--ABCD的底面是正方形,PD⊥底面ABCD,点E为PB的中点.且PD= 如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.
如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.