题目内容
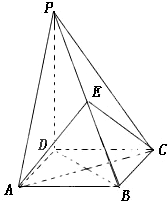 如图,四棱锥P--ABCD的底面是正方形,PD⊥底面ABCD,点E为PB的中点.且PD=
如图,四棱锥P--ABCD的底面是正方形,PD⊥底面ABCD,点E为PB的中点.且PD=| 2 |
(1)求证:平面AEC⊥平面PDB;
(2)求AE与平面PDB所成的角的大小.
考点:直线与平面所成的角,平面与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)欲证平面AEC⊥平面PDB,根据面面垂直的判定定理可知在平面AEC内一直线与平面PDB垂直,而根据题意可得AC⊥平面PDB;
(2)连接AC,BD,交于O,连接OE,则∠AEO为AE与平面PDB所成的角,求出AO,AE,即可得到结论.
(2)连接AC,BD,交于O,连接OE,则∠AEO为AE与平面PDB所成的角,求出AO,AE,即可得到结论.
解答:
(1)证明:∵四边形ABCD是正方形,∴AC⊥BD,
∵PD⊥底面ABCD,
∴PD⊥AC,∴AC⊥平面PDB,
∴平面AEC⊥平面PDB;
(2)解:连接AC,BD,交于O,连接OE,则
∵PD⊥底面ABCD,AC?底面ABCD,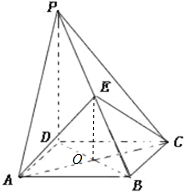
∴PD⊥AC,
∵四棱锥P-ABCD的底面是正方形,
∴AC⊥BD
∵PD∩BD=D
∴AC⊥平面PDB
∴∠AEO为AE与平面PDB所成的角,
设AB=a,则PD=
a,∴OE=
a
∵AO=
a,∴AE=a,
∴sin∠AEO=
=
,
∴∠AEO=45°
∵PD⊥底面ABCD,
∴PD⊥AC,∴AC⊥平面PDB,
∴平面AEC⊥平面PDB;
(2)解:连接AC,BD,交于O,连接OE,则
∵PD⊥底面ABCD,AC?底面ABCD,

∴PD⊥AC,
∵四棱锥P-ABCD的底面是正方形,
∴AC⊥BD
∵PD∩BD=D
∴AC⊥平面PDB
∴∠AEO为AE与平面PDB所成的角,
设AB=a,则PD=
| 2 |
| ||
| 2 |
∵AO=
| ||
| 2 |
∴sin∠AEO=
| AO |
| AE |
| ||
| 2 |
∴∠AEO=45°
点评:本题主要考查了直线与平面垂直的判定,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
命题p:?x∈R,log2x>0,命题q:?x0∈R,2x0<0,则下列命题为真命题的是( )
| A、p∨q | B、p∧q |
| C、(¬p)∧q | D、p∨(¬q) |
阅读如图所示的程序框图,则输出结果S的值为( )
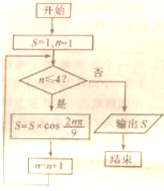

A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知函数f(x)=
,记f1(x)=f(x),f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,则f2014(10)=( )
|
| A、10 | B、lg110 | C、0 | D、1 |
“a>1”是“函数f(x)=x3+a在R上为单调递增函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
函数y=x2lg
的图象( )
| x-2 |
| x+2 |
| A、关于x轴对称 |
| B、关于原点对称 |
| C、关于直线y=x对称 |
| D、关于y轴对称 |