题目内容
20.已知P是抛物线y2=4x上一动点,则点P到直线l:2x-y+3=0和直线x=-2的距离之和的最小值是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}+1$ | C. | 2 | D. | $\sqrt{5}$-1 |
分析 由题意可知:点P到直线2x-y+3=0的距离为丨PA丨,点P到x=-2的距离为丨PD丨=丨PB丨+1,则点P到直线l:2x-y+3=0和x=-2的距离之和为丨PF丨+丨PA丨+1,当A,P和F共线时,点P到直线l:2x-y+3=0和直线x=-2的距离之和的最小,利用点到直线的距离公式,即可求得答案.
解答 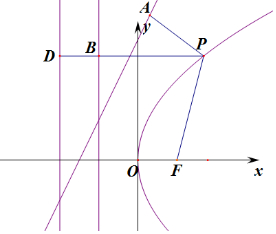 解:由抛物线的方程,焦点F(1,0),
解:由抛物线的方程,焦点F(1,0),
准线方程=-1,根据题意作图如右图,
点P到直线2x-y+3=0的距离为丨PA丨,
点P到x=-2的距离为丨PD丨=丨PB丨+1;
而由抛物线的定义知:丨PB丨=丨PF丨,
故点P到直线l:2x-y+3=0和x=-2的距离之和为
丨PF丨+丨PA丨+1,
而点F(1,0),到直线l:2x-y+3=0的距离为$\frac{丨2-0+3丨}{\sqrt{{2}^{2}+1}}$=$\sqrt{5}$,
P到直线l:2x-y+3=0和直线x=-2的距离之和的最小值$\sqrt{5}$+1,
故选B.
点评 本题考查抛物线的定义的应用及简单几何性质,考查点到直线的距离公式,考查计算能力,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
15.如图,扇形的半径为1,圆心角∠BAC=150°,点P在弧BC上运动,$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则$\sqrt{3}m-n$的最大值是( )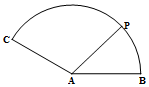

| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
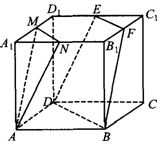 如图,已知棱长为4的正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1D1,A1B1,D1C1,B1C1的中点,求证:平面AMN∥平面EFBD.
如图,已知棱长为4的正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1D1,A1B1,D1C1,B1C1的中点,求证:平面AMN∥平面EFBD.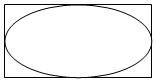 如图,矩形长为5,宽为3,在矩形内随机撒100颗黄豆,数得落在椭圆内的黄豆数为60颗,以此实验数据为依据可以估算椭圆的面积约为( )
如图,矩形长为5,宽为3,在矩形内随机撒100颗黄豆,数得落在椭圆内的黄豆数为60颗,以此实验数据为依据可以估算椭圆的面积约为( )