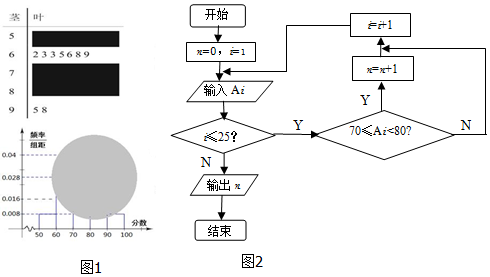
题目内容
15.如图,扇形的半径为1,圆心角∠BAC=150°,点P在弧BC上运动,$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则$\sqrt{3}m-n$的最大值是( )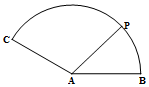
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
分析 建立坐标系,求出向量坐标,设P(cosθ,sinθ),根据向量坐标的运算得到m=cosθ+$\sqrt{3}$sinθ,n=2sinθ,则$\sqrt{3}m-n$=2sin(θ+60°),根据三角函数的性质即可求出最值.
解答 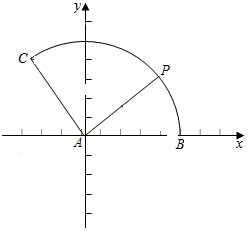 解:以AB为x轴,以A为原点,建立坐标系,
解:以AB为x轴,以A为原点,建立坐标系,
如图:P(cosθ,sinθ),0°≤θ≤150°,
则A(0,0),B(1,0),C(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
∵$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$,
∴(cosθ,sinθ)=m(1,0)+n(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)
=(m-$\frac{\sqrt{3}}{2}$n,$\frac{n}{2}$),
∴cosθ=m-$\frac{\sqrt{3}}{2}$n,sinθ=$\frac{n}{2}$,
∴m=cosθ+$\sqrt{3}$sinθ,n=2sinθ,
∴$\sqrt{3}m-n$=$\sqrt{3}$cosθ+3sinθ-2sinθ=$\sqrt{3}$cosθ+sinθ
=2sin(θ+60°),
∵0°≤θ≤150°,
∴60°≤θ+60°≤210°,
∴当θ=30°时,$\sqrt{3}m-n$的最大值为2,
故选:C.
点评 本题考查了向量的坐标运算和三角函数的性质,属于中档题.

练习册系列答案
相关题目
5.已知抛物线y2=2px的准线方程是x=-2,则p的值为( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
6.定义在区间(0,+∞)上的函数f(x)使不等式xf'(x)<4f(x)恒成立,其中f'(x)为f(x)的导数,则( )
| A. | $\frac{f(2)}{f(1)}<16$ | B. | $\frac{f(2)}{f(1)}<8$ | C. | $\frac{f(2)}{f(1)}<4$ | D. | $\frac{f(2)}{f(1)}<2$ |
10.集合M={x|lg(1-x)<1},N={x|-1≤x≤1},则M∩N=( )
| A. | (-9,1) | B. | (-9,1] | C. | [-1,1] | D. | [-1,1) |
20.已知P是抛物线y2=4x上一动点,则点P到直线l:2x-y+3=0和直线x=-2的距离之和的最小值是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}+1$ | C. | 2 | D. | $\sqrt{5}$-1 |
4.直线2x-y-3=0的倾斜角为θ,则tanθ=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 2 | D. | -2 |
5.函数$y=\sqrt{{{log}_{\frac{1}{2}}}(x-1)}$的定义域是( )
| A. | (1,+∞) | B. | (1,2] | C. | (1,2) | D. | (2,+∞) |