题目内容
若对于一切实数x,y,都有f(x+y)=f(x)+f(y):
(1)求f(0),并证明f(x)为奇函数;
(2)若f(1)=3,求f(-5).
(1)求f(0),并证明f(x)为奇函数;
(2)若f(1)=3,求f(-5).
考点:抽象函数及其应用,函数奇偶性的判断,函数的值
专题:函数的性质及应用
分析:(1)利用已知条件直接反证法,求f(0),然后通过反证法结合函数的奇偶性的定义,证明f(x)为奇函数;
(2)通过已知条件化简f(-5=5f(-1),利用f(1)=3,即可求f(-5).
(2)通过已知条件化简f(-5=5f(-1),利用f(1)=3,即可求f(-5).
解答:
解:(1)由于对一切实数x,y,都有f(x+y)=f(x)+f(y),
故在上式中可令x=y=0,则有:f(0+0)=f(0)+f(0),所以f(0)=0.…(2分)
再令 y=-x,则有:f[x+(-x)]=f(x)+f(-x),
所以:f(x)+f(-x)=f(0)=0,即f(-x)=-f(x),f(x)为奇函数.…(5分)
(2)由于f(x)为奇函数,且f(x+y)=f(x)+f(y),
f(-5)=f[(-1)+(-1)+(-1)+(-1)+(-1)]=f(-1)+f(-1)+f(-1)+f(-1)+f(-1)
=5f(-1)=-f(1)=-5×3=-15…(8分)
故在上式中可令x=y=0,则有:f(0+0)=f(0)+f(0),所以f(0)=0.…(2分)
再令 y=-x,则有:f[x+(-x)]=f(x)+f(-x),
所以:f(x)+f(-x)=f(0)=0,即f(-x)=-f(x),f(x)为奇函数.…(5分)
(2)由于f(x)为奇函数,且f(x+y)=f(x)+f(y),
f(-5)=f[(-1)+(-1)+(-1)+(-1)+(-1)]=f(-1)+f(-1)+f(-1)+f(-1)+f(-1)
=5f(-1)=-f(1)=-5×3=-15…(8分)
点评:本题考查抽象函数的应用,函数的奇偶性的证明,考查计算能力.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
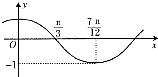
函数的图象如图所示,为了得到的图象,则只要将f(x)=cos2x的函数的图象( )

A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
在映射f:A→B中,A=B=R,且f:(x,y)→(x-y,x+y),则与A中的元素(2,1)在B中的象为( )
| A、(-3,1) |
| B、(1,3) |
| C、(-1,-3) |
| D、(3,1) |
 已知圆O:x2+y2=4,圆O与x轴交于A、B两点,过点B的圆的切线为l,P是圆上异于A、B的一点,PH垂直于x轴,垂足为H,E是PH的中点,延长AP,AE分别交l于F,C.
已知圆O:x2+y2=4,圆O与x轴交于A、B两点,过点B的圆的切线为l,P是圆上异于A、B的一点,PH垂直于x轴,垂足为H,E是PH的中点,延长AP,AE分别交l于F,C.