题目内容
已知f（x）=ax5+bx3+cx-4其中a，b为常数，若f（-2）=2，则f（2）的值等于（ ）
| A、-2 | B、-4 | C、-6 | D、-10 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：利用函数g（x）═ax5+bx3+cx的奇偶性，结合f（-2）=2，可求f（2）．
解答：
解：令函数g（x）═ax5+bx3+cx，显然函数g（x）═ax5+bx3+cx是奇函数，f（-2）=g（-2）-4=2，
g（-2）=-6，
f（2）=g（2）-4，g（-2）=-g（2），
∴f（2）=-g（-2）-4=-6-4=-10．
故选：D．
g（-2）=-6，
f（2）=g（2）-4，g（-2）=-g（2），
∴f（2）=-g（-2）-4=-6-4=-10．
故选：D．
点评：本题考查奇函数性质的应用，注意灵活解题．
练习册系列答案
相关题目
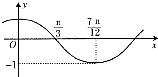
函数的图象如图所示，为了得到的图象，则只要将f（x）=cos2x的函数的图象（ ）
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
下列函数中，满足“?x1，x2∈（0，+∞）且x1≠x2，有（x1-x2）[f（x1）-f（x2）]＜0”的是（ ）
| A、f（x）=2x | ||
| B、f（x）=-（x-1）2 | ||
C、f（x）=
| ||
| D、f（x）=ln（x+1） |
某质点在25S内运动速度V是时间t的函数，它的图象如图所示，用解析法表示出这个函数，并求出6S时质点的速度．在映射f：A→B中，A=B=R，且f：（x，y）→（x-y，x+y），则与A中的元素（2，1）在B中的象为（ ）
| A、（-3，1） |
| B、（1，3） |
| C、（-1，-3） |
| D、（3，1） |
已知圆O：x2+y2=4，圆O与x轴交于A、B两点，过点B的圆的切线为l，P是圆上异于A、B的一点，PH垂直于x轴，垂足为H，E是PH的中点，延长AP，AE分别交l于F，C．