题目内容

已知函数f（x）=ax5-bx3+cx，f（-3）=2，则f（3）的值为（　　）
A、.2B、-2C、6D、-6
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：函数f（x）=ax5-bx3+cx，可判断奇函数，运用奇函数定义式求解即可．
解答： 解：∵函数f（x）=ax5-bx3+cx，∴f（-x）=-f（x）
∵f（-3）=2，∴f（3）=-2，
故选：B
点评：本题考查了运用奇函数的定义求解函数值，很容易．
练习册系列答案
相关题目
在直角坐标系xOy中，直线l经过点P（-1，0），其倾斜角为α，以原点O为极点，以x轴非负半轴为极轴，与直角坐标系xOy取相同的长度单位，建立极坐标系，设曲线C的极坐标方程为ρ2-6ρcosθ+5=0，若直线l与曲线C有公共点，则α的取值范围是（　　）
A、（0，
π
6
）
B、[
π
6
，
5π
6
]
C、（
π
6
，
π
3
]∪[
2π
3
，
5π
6
]
D、[0，
π
6
]∪[
5π
6
，π）
已知{an}为等比数列且an＞0，a1=1，a5=256；Sn为等差数列{bn}的前n项和，b1=2，5S5=2S8．
（Ⅰ）求{an}和{bn}的通项公式；
（Ⅱ）设Tn=a1b1+a2b2+…+anbn，求Tn．
已知函数f（x）满足2f（x）+f（
1
x
）=6x+
3
x
，对x≠0恒成立，则f（3）=
 
．
阅读如图所示的程序框图，若输入m=4，n=3，则输出的S=
 
．
函数的图象如图所示，为了得到的图象，则只要将f（x）=cos2x的函数的图象（　　）
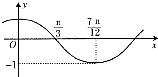
A、向右平移
π
6
个单位
B、向右平移
π
12
个单位
C、向左平移
π
6
个单位
D、向左平移
π
12
个单位
已知函数f（x）=
3
sin（π+x）sin（
3π
2
-x）-cos2x．
（1）求函数f（x）的最小正周期；
（2）若α∈[-
π
2
，0]，f（
1
2
α+
π
3
）=
1
10
，求tanα的值．
设函数f（x）=sin（ωx+
π
6
）-2sin2
ω
2
x+1（ω＞0），直线y=-
3
与函数f（x）图象相邻两交点的距离为π．
（1）求ω的值．
（2）在△ABC中，角A、B、C所对的边分别是a、b、c，若点（B，0）是函数y=f（x）图象的一个对称中心，且b=3，求△ABC面积的最大值．
已知函数f（x）=（-x2+ax）ex（a∈R，e为自然对数的底数）
（1）若函数f（x）在x=0处的切线方程与直线x+2y-1=0垂直，求a的值；
（2）求函数f（x）的单调区间，
（3）若函数f（x）在x∈（-1，1）上单调递增，则a的取值范围是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网