题目内容
12.已知函数f(x),对任意的实数x满足f(x-2)=f(x+2),且当x∈[-1,3)时,f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}}(-1≤x≤1)}\\{-|x-2|(1<x<3)}\end{array}\right.$,若直线y=kx与函数f(x)的图象有5个公共点,则实数k的取值范围是(-$\frac{\sqrt{15}}{15}$,-$\frac{1}{5}$)∪($\frac{1}{5}$,$\frac{\sqrt{15}}{15}$).分析 可判断函数f(x)的周期为4,从而作出函数f(x)与直线y=kx的图象,利用数形结合求解.
解答 解:∵对任意的实数x满足f(x-2)=f(x+2),
∴函数f(x)的周期为4,
作函数f(x)与直线y=kx的图象如下,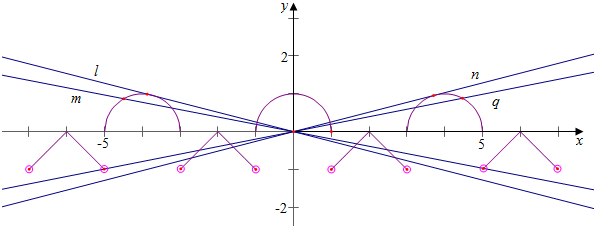 ,
,
结合图象可知,
kl=-$\frac{1}{\sqrt{{4}^{2}-1}}$=-$\frac{\sqrt{15}}{15}$,km=-$\frac{1}{5}$,kn=$\frac{1}{\sqrt{{4}^{2}-1}}$=$\frac{\sqrt{15}}{15}$,kq=$\frac{1}{5}$,
故实数k的取值范围是
(-$\frac{\sqrt{15}}{15}$,-$\frac{1}{5}$)∪($\frac{1}{5}$,$\frac{\sqrt{15}}{15}$);
故答案为:(-$\frac{\sqrt{15}}{15}$,-$\frac{1}{5}$)∪($\frac{1}{5}$,$\frac{\sqrt{15}}{15}$).
点评 本题考查了函数的性质的判断与应用,同时考查了学生的作图能力及数形结合的思想应用.

练习册系列答案
相关题目
17.设条件p:2x2-3x+1>0,条件q:$\frac{1}{x}$<1,则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
7.已知$U=\{y|y={2^x},x≥-1\},A=\{x|\frac{1}{x-1}≥1\}$,则∁UA=( )
| A. | $[\frac{1}{2},2]$ | B. | [2,+∞) | C. | $[\frac{1}{2},1]∪(2,+∞)$ | D. | $[\frac{1}{2},2)∪(2,+∞)$ |
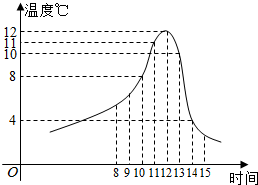 某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=$\left\{\begin{array}{l}{64,x≤0}\\{{2}^{kx+6},x>0}\end{array}\right.$且该食品在4℃的保鲜时间是16小时.已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,给出以下四个结论:
某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=$\left\{\begin{array}{l}{64,x≤0}\\{{2}^{kx+6},x>0}\end{array}\right.$且该食品在4℃的保鲜时间是16小时.已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,给出以下四个结论: