题目内容
已知m>0,p:(x+2)(x-3)≤0,q:1-m≤x≤1+m.
(I)若¬q是¬p的必要条件,求实数m的取值范围;
(II)若m=7,“p或q”为真命题,“p且q”为假命题,求实数x的取值范围.
(I)若¬q是¬p的必要条件,求实数m的取值范围;
(II)若m=7,“p或q”为真命题,“p且q”为假命题,求实数x的取值范围.
考点:必要条件、充分条件与充要条件的判断,命题的真假判断与应用
专题:计算题
分析:(I)m>0,p:(x+2)(x-3)≤0,q:1-m≤x≤1+m,分别求出命题p和q,根据¬q是¬p的必要条件,可得q⇒p,从而求出m的范围;
(II)m=7,代入命题q,求出m的范围,“p或q”为真命题,“p且q”为假命题,可知p与q一真一假,分类讨论进行求解;
(II)m=7,代入命题q,求出m的范围,“p或q”为真命题,“p且q”为假命题,可知p与q一真一假,分类讨论进行求解;
解答:
解:(I)m>0,p:(x+2)(x-3)≤0,q:1-m≤x≤1+m,
∴p:-2≤x≤3,q:1-m≤x≤1+m,
∵¬q是¬p的必要条件,q⇒p,
∴
解得m≤2,
当m=2时,q:-1≤x≤3,满足题意;
综上:0<m≤2;
(II)若m=7,可得q:-6≤x≤8,
∵“p或q”为真命题,“p且q”为假命题,
∴p与q有一个为真,一个为假,∵p:-2≤x≤3,
若p真q假可得,x为空集;
若p假q真可得,-6≤x<-2或3<x≤8;
∴p:-2≤x≤3,q:1-m≤x≤1+m,
∵¬q是¬p的必要条件,q⇒p,
∴
|
当m=2时,q:-1≤x≤3,满足题意;
综上:0<m≤2;
(II)若m=7,可得q:-6≤x≤8,
∵“p或q”为真命题,“p且q”为假命题,
∴p与q有一个为真,一个为假,∵p:-2≤x≤3,
若p真q假可得,x为空集;
若p假q真可得,-6≤x<-2或3<x≤8;
点评:此题主要考查命题真假的判断,以及充分必要条件的定义,解题过程中用到了分类讨论的思想,是一道基础题;

练习册系列答案
相关题目
二次函数y=a(a+1)x2-(2a+1)x+1,当a=1,2,3,…,n,…时,其图象在x轴上截得的弦长依次为d1,d2,…,dn,…,则d1+d2+…+dn为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如果a
=b(a>0,且a≠1),则( )
| 1 |
| 2 |
A、log
| ||||
B、log
| ||||
C、log
| ||||
D、log
|
若实数x,y满足不等式
,则z=2x+y的最大值为( )
|
| A、1 | B、3 | C、4 | D、5 |
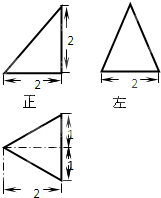
已知某个几何体的三视图如右,那么可得这个几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
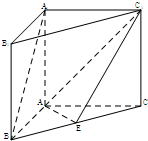 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.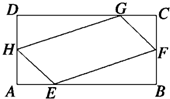 如图所示,在矩形ABCD中,已知AB=a,BC=b(b<a),AB,AD,CD,CB上分别截取AE,AH,CG,CF都等于x,记四边形EFGH的面积为f(x).
如图所示,在矩形ABCD中,已知AB=a,BC=b(b<a),AB,AD,CD,CB上分别截取AE,AH,CG,CF都等于x,记四边形EFGH的面积为f(x).