Question

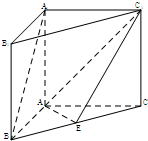如图，在直三棱柱ABC-A₁B₁C₁中，∠BAC=90°，AB=AC=AA₁=2，E是BC中点．
（Ⅰ）求证：A₁B∥平面AEC₁；
（Ⅱ）若棱AA₁上存在一点M，满足B₁M⊥C₁E，求AM的长；
（Ⅲ）求平面AEC₁与平面ABB₁A₁所成锐二面角的余弦值．

Answer 1

考点：二面角的平面角及求法,直线与平面平行的判定,点、线、面间的距离计算

专题：综合题,空间位置关系与距离,空间角

分析：（I）连接A₁C交AC₁于点O，连接EO，由ACC₁A₁为正方形，知O为A₁C中点，由E为CB中点，知EO∥A₁B，由此能够证明A₁B∥平面AEC₁．
（Ⅱ）以A为原点，AB为x轴，AC为y轴，AA₁为z轴建立空间直角坐标系，利用向量法能得到棱AA₁上存在一点M，满足B₁M⊥C₁E，并能求出AM的长
（Ⅲ）由

AE

=（1，1，0），

AC1

=（0，2，2），求出平面AEC₁的法向量为

n

=（1，-1，1），利用向量法能求出平面AEC₁与平面ABB₁A₁所成锐二面角的余弦值．

解答： （本小题满分14分）
（I）证明：连接A₁C交AC₁于点O，连接EO，
因为ACC₁A₁为正方形，所以O为A₁C中点，
又E为CB中点，所以EO为△A₁BC的中位线，
所以EO∥A₁B，…（2分）
又∵EO?平面AEC₁，A₁B?平面AEC₁，
所以A₁B∥平面AEC₁．…（4分）
（Ⅱ）解：以A为原点，AB为x轴，AC为y轴，AA₁为z轴建立空间直角坐标系
所以A（0，0，0），A₁（0，0，2），B（2，0，0），B₁（2，0，2），C₁（0，2，2），E（1，1，0），
设M（0，0，m），0≤m≤2，所以

B1M

=(-2，0，m-2)，

C1E

=（1，-1，-2），
因为B₁M⊥C₁E，所以

B1M

•

C1E

=0，解得m=1，所以AM=1．…（8分）
（Ⅲ）解：因为

AE

=（1，1，0），

AC1

=（0，2，2），
设平面AEC₁的法向量为

n

=（x，y，z），
则有

AE • n =0 AC1 • n =0

，得

x+y=0 y+z=0

，
令y=-1，则x=1，z=1，所以取

n

=（1，-1，1），…（10分）
因为AC⊥平面ABB₁A₁，取平面ABB₁A₁的法向量为

AC

=（0，2，0），…（11分）
所以cos＜

AC

，

n

＞=

AC • n

| AC |•| n |

=-

3

3

，…（13分）
平面AEC₁与平面ABB₁A₁所成锐二面角的余弦值为

3

3

．…（14分）

点评：本题考查直线与平面平行的证明，考查满足条件的点的判断，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．