题目内容
给出下列命题：
①“x=2”是“x2=4”的充分不必要条件；
②设A={x||x|≤3}，B={y|y=-x2+t}，若A∩B=∅，则实数t的取值范围为[3，+∞）；
③若log2x+logx2≥2，则x＞1；
④存在x，y∈R，使sin（x-y）=sinx-siny；
⑤若命题p：对任意的x∈R，函数y=cos（2x-
）的递减区间为[kπ-
，kπ+
]（k∈Z），命题q：存在x∈R使tanx=1，则命题“p且q”是真命题．
其中真命题的序号为（ ）
①“x=2”是“x2=4”的充分不必要条件；
②设A={x||x|≤3}，B={y|y=-x2+t}，若A∩B=∅，则实数t的取值范围为[3，+∞）；
③若log2x+logx2≥2，则x＞1；
④存在x，y∈R，使sin（x-y）=sinx-siny；
⑤若命题p：对任意的x∈R，函数y=cos（2x-
| π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
其中真命题的序号为（ ）
| A、①②④ | B、③④⑤ |
| C、②③⑤ | D、①③④ |
考点：命题的真假判断与应用
专题：简易逻辑
分析：①，利用充分必要条件的概念可判断知x=2⇒x2=4，反之，不行，可判断①；
②，依题意，可求得A={x|-3≤x≤3}，又B={y|y=-x2+t}，A∩B=∅，可求得实数t的取值范围为t＞12或t＜-3，可判断②；
③，利用对数函数的性质及基本不等式，可判断③；
④，举例x=0，y=0∈R，使sin（x-y）=sinx-siny，可判断④；
⑤，先利用余弦函数的单调性，求得函数y=cos（2x-
）的递减区间，可判断命题p为假命题，从而可判断命题“p且q”是假命题，可判断⑤．
②，依题意，可求得A={x|-3≤x≤3}，又B={y|y=-x2+t}，A∩B=∅，可求得实数t的取值范围为t＞12或t＜-3，可判断②；
③，利用对数函数的性质及基本不等式，可判断③；
④，举例x=0，y=0∈R，使sin（x-y）=sinx-siny，可判断④；
⑤，先利用余弦函数的单调性，求得函数y=cos（2x-
| π |
| 3 |
解答：
解：对于①，x=2⇒x2=4，充分性成立，反之，不然，必要性不成立，故①正确；
对于②，由|x|≤3得：-3≤x≤3，即A={x|-3≤x≤3}；
又B={y|y=-x2+t}，A∩B=∅，
∴y=-x2+t＞3或y=-x2+t＜-3恒成立，即t＞3+x2，或t＜x2-3（-3≤x≤3）恒成立，
∴t＞12或t＜-3，故②错误；
则实数t的取值范围为[3，+∞）；
对于③，∵log2x与logx2互为倒数，
∴当log2x+logx2≥2时，必有log2x＞0且log2x=1，即x=2时取“=”，所以x＞1，故③正确；
对于④，存在x=0，y=0∈R，使sin（0-0）=sin0-sin0成立，故④正确；
对于⑤，由2kπ≤2x-
≤2kπ+π（k∈Z）得：kπ+
≤x≤kπ+
（k∈Z），
∴函数y=cos（2x-
）的递减区间为[kπ+
，kπ+
]（k∈Z），即命题p为假命题，于是命题“p且q”是假命题，故⑤错误．
综上所述，真命题的序号为①③④，
故选：D．
对于②，由|x|≤3得：-3≤x≤3，即A={x|-3≤x≤3}；
又B={y|y=-x2+t}，A∩B=∅，
∴y=-x2+t＞3或y=-x2+t＜-3恒成立，即t＞3+x2，或t＜x2-3（-3≤x≤3）恒成立，
∴t＞12或t＜-3，故②错误；
则实数t的取值范围为[3，+∞）；
对于③，∵log2x与logx2互为倒数，
∴当log2x+logx2≥2时，必有log2x＞0且log2x=1，即x=2时取“=”，所以x＞1，故③正确；
对于④，存在x=0，y=0∈R，使sin（0-0）=sin0-sin0成立，故④正确；
对于⑤，由2kπ≤2x-
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
∴函数y=cos（2x-
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
综上所述，真命题的序号为①③④，
故选：D．
点评：本题考查命题的真假判断与应用，综合考查充分必要条件的概念、复合命题的真假判断，考查基本不等式的应用与集合的运算，属于难题．
练习册系列答案
相关题目
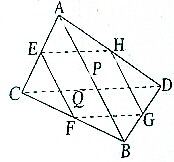如图所示，线段AB、CD所在直线是异面直线，E、F、G、H分别是线段AC、CB、BD、DA的中点．