题目内容
3.已知函数f(x)=(m2+m)x${\;}^{{m}^{2}-2m-1}$(m∈R),分别求m的取值范围.(1)f(x)为正比例函数;
(2)f(x)为反比例函数;
(3)f(x)在(0,+∞)上为增函数.
分析 (1)利用f(x)为正比例函数;列出方程求出m的范围即可.
(2)利用f(x)为反比例函数;列出方程求解即可.
(3)f(x)在(0,+∞)上为增函数.利用组合数的定义求解即可.
解答 解:(1)f(x)=(m2+m)x${\;}^{{m}^{2}-2m-1}$,
f(x)为正比例函数;可知:m2-2m-1=1,并且m2+m≠0,解得m=1±$\sqrt{3}$.
(2)函数f(x)=(m2+m)x${\;}^{{m}^{2}-2m-1}$(m∈R),f(x)为反比例函数;
可知:m2-2m-1=-1,并且m2+m≠0,解得m=2.
(3)函数f(x)=(m2+m)x${\;}^{{m}^{2}-2m-1}$,f(x)在(0,+∞)上为增函数.
可得函数f′(x)=(m2+m)(m2-2m-1)${x}^{{m}^{2}-2m-2}$>0在(0,+∞)上恒成立.
即:(m2+m)(m2-2m-1)>0,可得:$\left\{\begin{array}{l}{{m}^{2}+m>0}\\{{m}^{2}-2m-1>0}\end{array}\right.$或$\left\{\begin{array}{l}{{m}^{2}+m<0}\\{{m}^{2}-2m-1<0}\end{array}\right.$,
解得:m<-1或m$>1+\sqrt{2}$或1-$\sqrt{2}<$m<0.
点评 本题考查函数的解析式的应用,函数的导数与函数的单调性的关系,考查计算能力以及转化思想的应用.

练习册系列答案
相关题目
18.一圆锥的母线长度为2,底面半径为$\sqrt{3}$,以该圆锥的顶点为球心、$\sqrt{3}$为半径的球的表面与该圆锥的表面的交线长度为( )
| A. | 3π | B. | 4π | C. | (3+2$\sqrt{2}$)π | D. | (3+$\sqrt{3}$)π |
15.已知x是非零实数,则“x>1”是“$\frac{1}{x}$<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
12.如图是某几何体的三视图,则该几何体的体积是( )
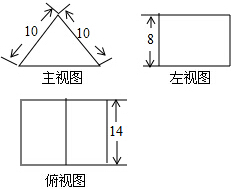

| A. | 672 | B. | 1120 | C. | 1344 | D. | 2016 |
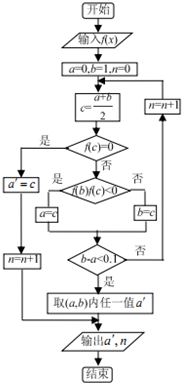 如图是用二分法求函数f(x)在区间(a,b)上的零点的程序框图,若输入的函数为f(x)=log2x+x-$\frac{1}{2}$,则输出的n的值为( )
如图是用二分法求函数f(x)在区间(a,b)上的零点的程序框图,若输入的函数为f(x)=log2x+x-$\frac{1}{2}$,则输出的n的值为( )