题目内容
10.已知等比数列{an}的首项a1=1,且a2、a4、a3成等差,则数列{an}的公比q=1或-$\frac{1}{2}$,若q<0,则数列{an}的前4项和S4=$\frac{5}{8}$.分析 由于a2、a4、a3成等差,可得2a4=a2+a3,a1=1,化简解得q.再利用等比数列的前n项和公式即可得出.
解答 解:∵a2、a4、a3成等差,
∴2a4=a2+a3,a1=1,
则2q3=q+q2,q≠0,化为2q2-q-1=0,
解得q=1,或-$\frac{1}{2}$.
q=-$\frac{1}{2}$时,S4=$\frac{1-(-\frac{1}{2})^{4}}{1-(-\frac{1}{2})}$=$\frac{5}{8}$.
故答案分别为:$1或-\frac{1}{2}$;$\frac{5}{8}$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.式子$\frac{1}{{2-{{cos}^2}θ}}$+$\frac{1}{{2-{{sin}^2}θ}}$(θ∈R)的最小值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
18.一圆锥的母线长度为2,底面半径为$\sqrt{3}$,以该圆锥的顶点为球心、$\sqrt{3}$为半径的球的表面与该圆锥的表面的交线长度为( )
| A. | 3π | B. | 4π | C. | (3+2$\sqrt{2}$)π | D. | (3+$\sqrt{3}$)π |
5.若某程序框图如图所示,则该程序运行后输出S的值为( )
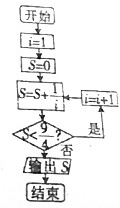

| A. | $\frac{147}{60}$ | B. | $\frac{17}{6}$ | C. | $\frac{25}{4}$ | D. | $\frac{137}{60}$ |
15.已知x是非零实数,则“x>1”是“$\frac{1}{x}$<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
19.设随机变量X服从正态分布N(2,22),则P(2<X<3)可以表示为( )
| A. | 1~P(X<1) | B. | $\frac{1-2P(X<1)}{2}$ | C. | P(0<X<1) | D. | $\frac{1+2P(X<1)}{2}$ |