题目内容
6.在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立直角坐标系,圆C的极坐标方程为ρ=2$\sqrt{2}$sin(θ-$\frac{π}{4}$),直线的参数方程为$\left\{\begin{array}{l}{x=t-1}\\{y=2t-1}\end{array}$(t为参数),直线和圆C交于A,B两点,P是圆C上不同于A,B的任意一点.(Ⅰ)求圆心的极坐标;
(Ⅱ)求△PAB面积的最大值.
分析 (I)求出圆C的直角坐标方程,得出圆心坐标,转化为极坐标;
(II)求出直线l的普通方程,圆心到直线的距离d,利用勾股定理求出|AB|,则△PAB在AB边上的高最大为d+r.
解答 解;(I)∵$ρ=2\sqrt{2}sin(θ-\frac{π}{4})$,∴ρ2=2ρsinθ-2ρcosθ,
∴圆C的直角坐标方程为x2+y2=2y-2x,即(x+1)2+(y-1)2=2.
∴圆C的圆心为C(-1,1),转化为极坐标为($\sqrt{2}$,$\frac{3π}{4}$).
(II)直线l的普通方程为2x-y+1=0,
∴圆心到直线l的距离d=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.又圆C的半径r=$\sqrt{2}$,
∴|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$=$\frac{2\sqrt{30}}{5}$,
∴当P到直线l的距离为d+r时,△PAB面积最大.
∴△PAB面积的最大值为$\frac{1}{2}$|AB|•(d+r)=$\frac{1}{2}•\frac{2\sqrt{30}}{5}•(\frac{2\sqrt{5}}{5}+\sqrt{2})$=$\frac{2\sqrt{6}+2\sqrt{15}}{5}$.
点评 本题考查了极坐标方程与直角坐标方程的转化,直线与圆的位置关系,属于中档题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
1.式子$\frac{1}{{2-{{cos}^2}θ}}$+$\frac{1}{{2-{{sin}^2}θ}}$(θ∈R)的最小值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
18.一圆锥的母线长度为2,底面半径为$\sqrt{3}$,以该圆锥的顶点为球心、$\sqrt{3}$为半径的球的表面与该圆锥的表面的交线长度为( )
| A. | 3π | B. | 4π | C. | (3+2$\sqrt{2}$)π | D. | (3+$\sqrt{3}$)π |
15.已知x是非零实数,则“x>1”是“$\frac{1}{x}$<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
16.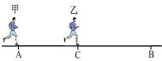 如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )
如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )
 如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )
如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )| A. | x1+x2 | B. | $\frac{({x}_{1}+{x}_{2})^{2}}{4{x}_{1}}$ | ||
| C. | $\frac{{x}_{1}^{2}}{4({x}_{1}+{x}_{2})}$ | D. | $\frac{({x}_{1}+{x}_{2})^{2}}{({x}_{1}-{x}_{2}){x}_{1}}$ |
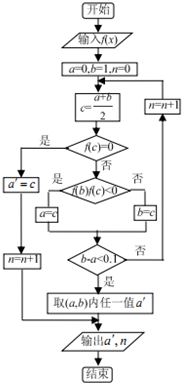 如图是用二分法求函数f(x)在区间(a,b)上的零点的程序框图,若输入的函数为f(x)=log2x+x-$\frac{1}{2}$,则输出的n的值为( )
如图是用二分法求函数f(x)在区间(a,b)上的零点的程序框图,若输入的函数为f(x)=log2x+x-$\frac{1}{2}$,则输出的n的值为( )