题目内容
以下有四种说法:
①若p或q为真,p且q为假,则p与q必为一真一假;
②若数列{an}的前n项和为Sn=n2+n+1,n∈N*,则an=2n,n∈N*;
③若实数t满足f(t)=-t,则称t是函数f(x)的一个次不动点,设函数f(x)=lnx与函数g(x)=ex(其中e为自然对数的底数)的所有次不动点之和为m,则m=0
④若定义在R上的函数f(x)满足f(x+2)=-f(x-1),则6为函数f(x)的周期.
以上四种说法,其中正确说法的序号为 .
①若p或q为真,p且q为假,则p与q必为一真一假;
②若数列{an}的前n项和为Sn=n2+n+1,n∈N*,则an=2n,n∈N*;
③若实数t满足f(t)=-t,则称t是函数f(x)的一个次不动点,设函数f(x)=lnx与函数g(x)=ex(其中e为自然对数的底数)的所有次不动点之和为m,则m=0
④若定义在R上的函数f(x)满足f(x+2)=-f(x-1),则6为函数f(x)的周期.
以上四种说法,其中正确说法的序号为
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①.利用“或”与“且”命题真假的判定方法可得:p与q必为一真一假;
②.利用n≥2时,an=Sn-Sn-1=2n,n=1时,a1=3,即可判断出;
③.由于函数f(x)=lnx与函数g(x)=ex互为反函数,关于直线y=x对称,可得所有次不动点之和为m=0;
④.由于f(x+6)=-f(x+3)=f(x),即可得出函数f(x)的周期是6.
②.利用n≥2时,an=Sn-Sn-1=2n,n=1时,a1=3,即可判断出;
③.由于函数f(x)=lnx与函数g(x)=ex互为反函数,关于直线y=x对称,可得所有次不动点之和为m=0;
④.由于f(x+6)=-f(x+3)=f(x),即可得出函数f(x)的周期是6.
解答:
解:对于①.若p或q为真,p且q为假,则p与q必为一真一假,正确;
对于②.若数列{an}的前n项和为Sn=n2+n+1,n∈N*,则n≥2时,an=Sn-Sn-1=2n,n=1时,a1=3,因此上式对于n=1不成立,不正确;
对于③.由于函数f(x)=lnx与函数g(x)=ex互为反函数,其图象关于直线y=x对称,因此所有次不动点之和为m=0,正确;
对于④.由定义在R上的函数f(x)满足f(x+2)=-f(x-1),∴f(x+6)=-f(x+3)=f(x),则函数f(x)的周期是6,正确.
以上四种说法,其中正确说法的序号为 ①③④.
故答案为:①③④.
对于②.若数列{an}的前n项和为Sn=n2+n+1,n∈N*,则n≥2时,an=Sn-Sn-1=2n,n=1时,a1=3,因此上式对于n=1不成立,不正确;
对于③.由于函数f(x)=lnx与函数g(x)=ex互为反函数,其图象关于直线y=x对称,因此所有次不动点之和为m=0,正确;
对于④.由定义在R上的函数f(x)满足f(x+2)=-f(x-1),∴f(x+6)=-f(x+3)=f(x),则函数f(x)的周期是6,正确.
以上四种说法,其中正确说法的序号为 ①③④.
故答案为:①③④.
点评:本题考查了简易逻辑的判定、等差数列的定义及其通项公式、反函数的性质、函数的周期性,考查了推理能力,属于中档题.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
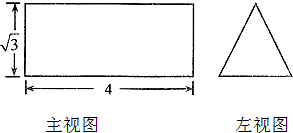 已知正三棱柱ABC-A′B′C′的主视图和侧左视图如图所示.设△ABC的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为( )
已知正三棱柱ABC-A′B′C′的主视图和侧左视图如图所示.设△ABC的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为( )| A、8 | B、4 | C、12 | D、16 |
设是虚数单位,若复数
为实数,则实数a的值为( )
| a-i |
| 2+i |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
已知
、
是平面向量,若
⊥(
-2
),
⊥(
-2
),则
与
的夹角是( )
| a |
| b |
| a |
| a |
| b |
| b |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
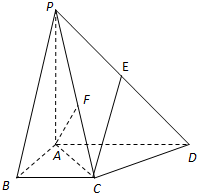 如图,在四棱锥P-ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2AB=2BC.BC∥AD,AB⊥AD.
如图,在四棱锥P-ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2AB=2BC.BC∥AD,AB⊥AD.