题目内容
数列{bn}(n∈N*)是递增的等比数列,且b1+b3=5,b1b3=4.数列{an}满足an=log2bn+3.
(Ⅰ)求数列{bn},{an}的通项公式:
(Ⅱ)设数列{an}的前n项和为Sn,是否存在正整数n,使得数列{
}前n项和为Tn满足Tn-(n-1)2=4025?若存在,求出n的值;若不存在,请说明理由.
(Ⅰ)求数列{bn},{an}的通项公式:
(Ⅱ)设数列{an}的前n项和为Sn,是否存在正整数n,使得数列{
| 4Sn-11n |
| n |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(I)设等比数列{bn}的公比为q,由于b1+b3=5,b1b3=4.b1<b3,解得b1=1,b3=4.利用b3=b1q2,q>0,解得q.可得bn.利用数列{an}满足an=log2bn+3.即可得出.
(II)利用等差数列的前n项和公式可得Sn,可得
=2n-1.可得Tn=n2.假设存在正整数n,使得数列{
}前n项和为Tn满足Tn-(n-1)2=4025,解出即可.
(II)利用等差数列的前n项和公式可得Sn,可得
| 4Sn-11n |
| n |
| 4Sn-11n |
| n |
解答:
解:(I)设等比数列{bn}的公比为q,
∵b1+b3=5,b1b3=4.b1<b3,解得b1=1,b3=4.
∴4=1×q2,q>0,解得q=2.
∴bn=2n-1.
∵数列{an}满足an=log2bn+3,
∴an=n-1+3=n+2.
(II)Sn=
,
∴
=
=2n-1.
∴Tn=
=n2.
假设存在正整数n,使得数列{
}前n项和为Tn满足Tn-(n-1)2=4025,
∴n2-(n-1)2=4025,
∴2n-1=4025,解得n=2013.
∴存在正整数n=2013,使得数列{
}前n项和为Tn满足Tn-(n-1)2=4025.
∵b1+b3=5,b1b3=4.b1<b3,解得b1=1,b3=4.
∴4=1×q2,q>0,解得q=2.
∴bn=2n-1.
∵数列{an}满足an=log2bn+3,
∴an=n-1+3=n+2.
(II)Sn=
| n(3+n+2) |
| 2 |
∴
| 4Sn-11n |
| n |
| 2n(n+5)-11n |
| n |
∴Tn=
| n(1+2n-1) |
| 2 |
假设存在正整数n,使得数列{
| 4Sn-11n |
| n |
∴n2-(n-1)2=4025,
∴2n-1=4025,解得n=2013.
∴存在正整数n=2013,使得数列{
| 4Sn-11n |
| n |
点评:本题考查了等比数列与等差数列的通项公式及其前n项和公式、对数的运算性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知
、
是平面向量,若
⊥(
-2
),
⊥(
-2
),则
与
的夹角是( )
| a |
| b |
| a |
| a |
| b |
| b |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
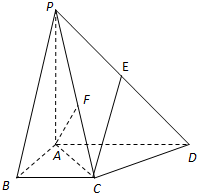 如图,在四棱锥P-ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2AB=2BC.BC∥AD,AB⊥AD.
如图,在四棱锥P-ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2AB=2BC.BC∥AD,AB⊥AD.