题目内容
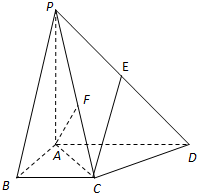
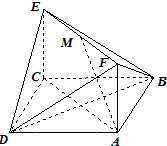 如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=| 2 |
(1)求证:AM∥平面BDE;
(2)在线段AC上是否存在一点P,使直线PF与AD所成角为60°?证明你的结论.
考点:直线与平面平行的判定,异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)记AC与BD的交点为O,连接OE,由已知O,M分别是AC,EF的中点,ACEF是矩形,容易得到AM∥OE,利用线面平行的性质可证;
(2)设CP=T(0≤T≤2),作PQ⊥AB于Q,则PQ∥AD,得到PQ⊥平面ABF,再由△PAQ为等腰直角三角形,△PAF为直角三角形,得到关于t的等式解之得到t=1即可.
(2)设CP=T(0≤T≤2),作PQ⊥AB于Q,则PQ∥AD,得到PQ⊥平面ABF,再由△PAQ为等腰直角三角形,△PAF为直角三角形,得到关于t的等式解之得到t=1即可.
解答:
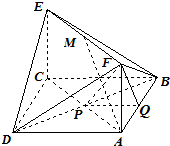 (1)证明:记AC与BD的交点为O,连接OE,
(1)证明:记AC与BD的交点为O,连接OE,
∵O,M分别是AC,EF的中点,ACEF是矩形,
∴四边形AOEM是平行四边形,
∴AM∥OE…(4分)
∵OE?平面BDE,AM?平面BDE,
∴AM∥平面BDE.…(6分)
(2)设CP=T(0≤T≤2),
作PQ⊥AB于Q,则PQ∥AD,
∵PQ⊥AB,PQ⊥AF,AB∩AF=A,
∴PQ⊥平面ABF,
QF?平面ABF,
∴PQ⊥QF.
在RT△PQF中,∠FPQ=60°,PF=2PQ.…(9分)
∵△PAQ为等腰直角三角形,
∴PQ=
(2-t)
又∵△PAF为直角三角形,
∴PF=
,
∴
=2-
(2-t),∴t=1或t=3(舍去).
∴点P是AC的中点.…(12分)
 (1)证明:记AC与BD的交点为O,连接OE,
(1)证明:记AC与BD的交点为O,连接OE,∵O,M分别是AC,EF的中点,ACEF是矩形,
∴四边形AOEM是平行四边形,
∴AM∥OE…(4分)
∵OE?平面BDE,AM?平面BDE,
∴AM∥平面BDE.…(6分)
(2)设CP=T(0≤T≤2),
作PQ⊥AB于Q,则PQ∥AD,
∵PQ⊥AB,PQ⊥AF,AB∩AF=A,
∴PQ⊥平面ABF,
QF?平面ABF,
∴PQ⊥QF.
在RT△PQF中,∠FPQ=60°,PF=2PQ.…(9分)
∵△PAQ为等腰直角三角形,
∴PQ=
| ||
| 2 |
又∵△PAF为直角三角形,
∴PF=
| (2-t)2+1 |
∴
| (2-t)2+1 |
| ||
| 2 |
∴点P是AC的中点.…(12分)
点评:本题考查了线面平行的判定以及线面垂直的性质的运用,结合等腰直角三角形的性质求t,体现了代数思想.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
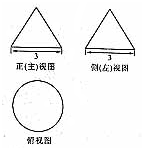 已知一个几何体的正(主)视图及侧(左)视图均是边长为3的正三角形,俯视图是直径为3的圆,则此几何体的体积为( )
已知一个几何体的正(主)视图及侧(左)视图均是边长为3的正三角形,俯视图是直径为3的圆,则此几何体的体积为( )A、
| ||||
| B、9π | ||||
C、
| ||||
| D、12π |
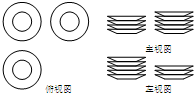 一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,三种视图如下所示,则这张桌子上碟子的个数为( )
一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,三种视图如下所示,则这张桌子上碟子的个数为( )| A、11 | B、12 | C、13 | D、14 |
 如图,在四棱锥P-ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2AB=2BC.BC∥AD,AB⊥AD.
如图,在四棱锥P-ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2AB=2BC.BC∥AD,AB⊥AD.