题目内容
已知函数f（x）=x+sinπx-3，则f（
）+f（
）+f（
）+…+f（
）的值为 ．
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4029 |
| 2015 |
考点：函数的值
专题：函数的性质及应用
分析：由已知得f（x）+f（2-x）=-4，从而f（
）+f（
）+f（
）+…+f（
）=-4×2014+f（1），由此能求出结果．
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4029 |
| 2015 |
解答：
解：∵函数f（x）=x+sinπx-3，
∴f（2-x）=2-x+sin（2π-πx）-3=2-x-sinπx-3，
∴f（x）+f（2-x）=-4，
∴f（
）+f（
）+f（
）+…+f（
）
=-4×2014+f（1）
=-8056+1+sinπ-3
=-8058．
故答案为：-8058．
∴f（2-x）=2-x+sin（2π-πx）-3=2-x-sinπx-3，
∴f（x）+f（2-x）=-4，
∴f（
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4029 |
| 2015 |
=-4×2014+f（1）
=-8056+1+sinπ-3
=-8058．
故答案为：-8058．
点评：本题考查函数值的求法，是中档题，解题时要认真审题，解题的关键是推导出f[x+（2-x）]=-4．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
方程4x-2x+1+4m=0只有一个实数解，则实数m的取值范围是（ ）
| A、{m|m≤0} | ||
B、{m|0＜m＜
| ||
C、{m|m＞
| ||
D、{m|m≤0或m=
|
方程|sinx|=kx（k＞0）有且仅有两个不同的非零实数解θ，Φ（θ＞Φ），则以下有关两根关系的结论正确的是（ ）
| A、sinΦ=Φcosθ |
| B、sinΦ=-Φcosθ |
| C、cosΦ=θsin |
| D、sinθ=-θsinΦ |
已知函数f（x）=lg（x-1），那么f（x）的定义域是（ ）
| A、R |
| B、{x|x＞1} |
| C、{x|x≠1} |
| D、{x|x≠0} |
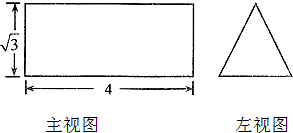已知正三棱柱ABC-A′B′C′的主视图和侧左视图如图所示．设△ABC的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，在旋转过程中对应的俯视图的面积为S，则S的最大值为（ ）
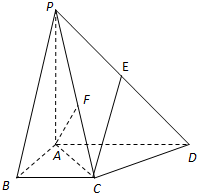如图，在四棱锥P-ABCD中，平面PAC⊥平面ABCD，且PA⊥AC，PA=AD=2AB=2BC．BC∥AD，AB⊥AD．