题目内容
16. 已知函数f(x)=2sin($\frac{1}{3}x-\frac{π}{6}$).
已知函数f(x)=2sin($\frac{1}{3}x-\frac{π}{6}$).(1)用“五点法”画出函数在一个周期内的图象;
(2)完整叙述函数f(x)=2sin($\frac{1}{3}x-\frac{π}{6}$)的图象可以由函数f(x)=2sinx的图象经过两步怎样的变换得到;
(3)求使f(x)≥0成立的取值集合.
解:(1)
| $\frac{1}{3}$x-$\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2 |
| x | $\frac{π}{2}$ | 2π | $\frac{7π}{2}$ | 5π | $\frac{13π}{2}$ |
| y | 0 | 2 | 0 | 2 | 0 |
分析 (1)根据五点法,求出函数的五点对应的坐标,即可得到结论.
(2)由条件利用y=Asin(ωx+φ)的图象变换规律,可得结论.
(3)由2sin($\frac{1}{3}x-\frac{π}{6}$)≥0,可得:2kπ≤$\frac{1}{3}x-\frac{π}{6}$≤π+2kπ,k∈Z,进而解得:$\frac{π}{2}$+6kπ≤x≤$\frac{7π}{2}$+6kπ,k∈Z,
即可得解.
解答 解:(1)列表如下:
| $\frac{1}{3}x-\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{2}$ | 2π | $\frac{7π}{2}$ | 5π | $\frac{13π}{2}$ |
| y | 0 | 2 | 0 | -2 | 0 |
 …6分
…6分(2)先把f(x)=2sinx的图象上所有的点向右平行移动$\frac{π}{6}$个单位长度,得到y=2sin(x-$\frac{π}{6}$)的图象,
再把所有点的横坐标伸长到原来的3倍(纵坐标不变),得到f(x)=2sin($\frac{1}{3}x-\frac{π}{6}$)的图象…10分
(3)由f(x)≥0,可得:2sin($\frac{1}{3}x-\frac{π}{6}$)≥0,可得:2kπ≤$\frac{1}{3}x-\frac{π}{6}$≤π+2kπ,k∈Z,
解得:$\frac{π}{2}$+6kπ≤x≤$\frac{7π}{2}$+6kπ,k∈Z,
∴f(x)≥0成立的取值集合是{x|$\frac{π}{2}$+6kπ≤x≤$\frac{7π}{2}$+6kπ,k∈Z}…14分
点评 本题主要考查三角函数图象的做法,y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,利用五点法是解决本题的关键.比较基础.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
2.已知集合A={x|0<x<3},B={x|(x+2)(x-1)>0},则A∩B等于( )
| A. | (0,3) | B. | (1,3) | C. | (2,3) | D. | (-∞,-2)∪(0,+∞) |
4.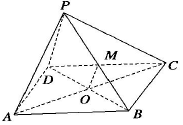 如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )
如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )
 如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )
如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下面四个命题:①OM∥面PCD;②OM∥面PBC;③OM∥面PDA;④OM∥面PBA.其中正确命题的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.已知log5[log3(log2x)]=0,那么x${\;}^{-\frac{1}{3}}$=( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
6.已知幂函数y=f(x)的图象过点($\frac{1}{4}$,4),则f(2)=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |